A simple eco-grammar system of type INS is a hybrid eco-grammar system
Simple eco-grammar systems with only INS- or with only REP-type agents are special cases of hybrid eco-grammar systems. In this part of the chapter we present some results about these homogeneous systems. The first results are almost direct consequences of the results presented in the first part of the chapter, we present them however again, because we find it worth showing the similarity between them and the results presented in Section 3.1.
Since in simple eco-grammar systems of type INS or REP the value of ![]() is
determined by the type of the system, we omit it in the notation and
thus a simple eco-grammar system of type INS or REP is denoted by
is
determined by the type of the system, we omit it in the notation and
thus a simple eco-grammar system of type INS or REP is denoted by
![]() .
.
Those simple eco-grammar systems, where the agents are represented by sets of CF rules will be referred as EG systems of type CF in this section.
We want to define the derivation mode ![]()
![]() for simple eco-grammar systems of
type INS and REP in the similar way as it was presented in
the CF case. We do not have to introduce this derivation mode
as a new one, because we can consider it as a special case of
Definition 4.3. In this way the same derivation mode is
defined as in Definition 3.1 for simple eco-grammar systems of type CF.
for simple eco-grammar systems of
type INS and REP in the similar way as it was presented in
the CF case. We do not have to introduce this derivation mode
as a new one, because we can consider it as a special case of
Definition 4.3. In this way the same derivation mode is
defined as in Definition 3.1 for simple eco-grammar systems of type CF.
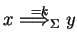 ),
if
),
if
 holds with the hybrid eco-grammar system
holds with the hybrid eco-grammar system
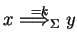 ),
if
),
if
 holds with the hybrid eco-grammar system
holds with the hybrid eco-grammar system
We denote the transitive and reflexive closure of
![]() by
by
![]() .
.

As already presented in Section 4.1,
the class of languages which can be generated by a
simple eco-grammar system of type ![]() is denoted by
is denoted by
![]() for
for
![]() CF
CF![]() INS
INS![]() REP
REP![]() .
The class of languages generated by systems containing
.
The class of languages generated by systems containing
![]() agents and
operating in the derivation mode
agents and
operating in the derivation mode ![]() is denoted by
is denoted by
![]() for
for
![]() CF
CF![]() INS
INS![]() REP
REP![]() .
.
In the following we
summarise some consequences of
Theorem 4.11.
In these results
language classes
![]() with fixed
with fixed ![]() (
(
![]() INS
INS![]() REP
REP![]() ) and
with different parameters
) and
with different parameters ![]() and
and ![]() , with
, with
![]() , are compared.
We can see that the results are similar to the ones presented in
Chapter 3 about EG systems of type CF.
, are compared.
We can see that the results are similar to the ones presented in
Chapter 3 about EG systems of type CF.
To begin with, results concerning simple eco-grammar systems of type INS are presented.
PROOF.
The incomparability also follows from the incomparability results of
Theorem 4.11 and from the above fact that we can
suppose that in a hybrid eco-grammar system working in the derivation mode
![]() there are only INS-type agents.height 5pt width 5pt depth 0pt
there are only INS-type agents.height 5pt width 5pt depth 0pt
About simple eco-grammar systems of type REP we have similar results.
PROOF.
Having examined the system and the derivation process, we can see that in the derivation mode
Requirements of Lemma 4.8 hold for the generated language
![]() and we note that
in the words being over the second sub-alphabet
and we note that
in the words being over the second sub-alphabet
![]() the only letter
the only letter ![]() precedes all occurrences of the letters
precedes all occurrences of the letters ![]() .
We also note that the distance between
.
We also note that the distance between ![]() and the
letters
and the
letters ![]() is not bounded in the words over
is not bounded in the words over
![]() , that is,
for any
, that is,
for any ![]() there exists a word over this
sub-alphabet where the sub-word between
there exists a word over this
sub-alphabet where the sub-word between ![]() and
the first letter
and
the first letter ![]() is longer than
is longer than
![]() .
.
PROOF.
We examine how the system ![]() can introduce letters
can introduce letters ![]() during
a derivation step
during
a derivation step
![]() where
where
![]() and
and
![]() .
.
So we have
![]() .
But we can also apply this rule
.
But we can also apply this rule
![]() to the first letter
to the first letter ![]() of a word in
of a word in ![]() and so we would get a word where a letter
and so we would get a word where a letter ![]() stands before
stands before ![]() .
It is a contradiction because
there are no words like this in
.
It is a contradiction because
there are no words like this in
![]() .
.
In the derivation mode
The requirements of Lemma 4.7 holds for the generated language
![]() and we note that
in the words being over the second sub-alphabet
and we note that
in the words being over the second sub-alphabet
![]() the
letters
the
letters ![]() can occur anywhere
after the sequence of letters
can occur anywhere
after the sequence of letters ![]() .
.
PROOF.
As mentioned above,
![]() has all the properties
required by Lemma 4.7, therefore we can say that
if
has all the properties
required by Lemma 4.7, therefore we can say that
if
 holds, then
holds, then
![]() and
and ![]() are over the different sub-alphabets
are over the different sub-alphabets
![]() and
and
![]() .
.
We examine the rules of ![]() which can be used to generate words
in
which can be used to generate words
in
![]() from words being over
from words being over
![]() .
These rules are in the form of
.
These rules are in the form of
![]() or
or
![]() ,
where
,
where
![]() .
.
(1)
(2)
(3)
(4)
(5)
where
![]() and
and
![]() .
.
In the cases (2), (3) and (4), a letter ![]() could stand before letters
could stand before letters ![]() if we use the rule
if we use the rule
![]() ,
, ![]() , of
, of ![]() .
.
So all the rules producing letters ![]() must be in the form of (1) or (5)
but from this fact it follows that
must be in the form of (1) or (5)
but from this fact it follows that ![]() must contain a deletion rule
in the form of
must contain a deletion rule
in the form of
![]() because this is the only way to introduce
a letter
because this is the only way to introduce
a letter ![]() just after the sequence of letters
just after the sequence of letters ![]() .
If there exists a deletion rule in
.
If there exists a deletion rule in ![]() in the form of
in the form of
![]() ,
then from a word long enough, being over
alph
,
then from a word long enough, being over
alph![]() , we
could derive a word which would contain a lot of letters
, we
could derive a word which would contain a lot of letters ![]() but only
a few letters
but only
a few letters ![]() (by using this deletion rule and the rule
(by using this deletion rule and the rule
![]() ,
, ![]() at the same step).
It is a contradiction because in
at the same step).
It is a contradiction because in
![]() , in each word, the number of
letters
, in each word, the number of
letters ![]() is at least the half of the number of letters
is at least the half of the number of letters ![]() .height 5pt width 5pt depth 0pt
.height 5pt width 5pt depth 0pt
In mode
The first few steps of a derivation in derivation mode

PROOF.
First,
we note that
letters ![]() can be introduced only by agents, otherwise more than
can be introduced only by agents, otherwise more than ![]() letters
letters ![]() could be in the generated words.
Hence letters
could be in the generated words.
Hence letters ![]() can be introduced only by the agent-rules
being in the form of
can be introduced only by the agent-rules
being in the form of
![]() , where
, where
![]() (since
we can apply Lemma 4.8 to
(since
we can apply Lemma 4.8 to
![]() with
alph
with
alph![]() ).
).
Since ![]() , there exist two different letters
, there exist two different letters ![]() in
in ![]() ,
, ![]() and
and ![]() , and these letters can occur at distance of any length
from each other in the words of
, and these letters can occur at distance of any length
from each other in the words of
![]() .
Therefore
.
Therefore ![]() is not possible.
Since
is not possible.
Since
![]() , for each letter
, for each letter ![]() there exists at most one
agent which can introduce this letter
there exists at most one
agent which can introduce this letter ![]() , otherwise words with
two letters
, otherwise words with
two letters ![]() with the same subscript could be generated.
with the same subscript could be generated.
One agent could not introduce two different letters ![]() either
because in this case the distance between these letters
either
because in this case the distance between these letters ![]() would be bounded in the generated words.
would be bounded in the generated words.
Thus in an agent-rule in the form of
![]()
![]()
![]() cannot contain a letter
cannot contain a letter ![]() ,
therefore
,
therefore
![]() ,
, ![]() .
Moreover,
.
Moreover, ![]() is not possible because in this case a letter
is not possible because in this case a letter ![]() could
stand at the first position of a generated word (by applying
this agent-rule to the first letter of a word).
could
stand at the first position of a generated word (by applying
this agent-rule to the first letter of a word).
Hence we obtain that any rule, used by the agents to introduce letters ![]() ,
is in the form of
,
is in the form of
![]() ,
, ![]() and
and
![]() .
But in this case words like
.
But in this case words like ![]() (
(
![]() are
impossible to derive,
which is a contradiction.
are
impossible to derive,
which is a contradiction.
2.
Let us suppose that
![]() holds
with a simple eco-grammar
system
holds
with a simple eco-grammar
system
![]() of type CF (where
of type CF (where
![]() is defined in
Example 4.25 above).
We can apply Lemma 4.8 to
is defined in
Example 4.25 above).
We can apply Lemma 4.8 to ![]() , so the words in a
derivation sequence are alternately over
, so the words in a
derivation sequence are alternately over
![]() and
and
![]() .
Following the line of the proof of Lemma 4.23, we can say that
the rules of
.
Following the line of the proof of Lemma 4.23, we can say that
the rules of ![]() used to produce words being over the sub-alphabet
used to produce words being over the sub-alphabet
![]() are either in the form
are either in the form
![]() or in the form
or in the form
![]() , where
, where ![]() .
We can also say that there are rules of the above form with
.
We can also say that there are rules of the above form with ![]() .
.
The agents can introduce letters ![]() only by rules in the form of
only by rules in the form of
![]() or
or
![]() , where
, where
![]() .
By applying a rule
.
By applying a rule
![]() to the first
to the first ![]() of a word of
of a word of
![]() and
the rule
and
the rule
![]() ,
, ![]() to all other letters
to all other letters ![]() which are
not concerned by the actions of the agents, we obtain a word where a
letter
which are
not concerned by the actions of the agents, we obtain a word where a
letter ![]() stands before a letter
stands before a letter ![]() .
Similarly, by applying a rule
.
Similarly, by applying a rule
![]() to the last letter
to the last letter ![]() and
the rule
and
the rule
![]() , with
, with ![]() , to the remaining letters
, to the remaining letters
![]() ,
we get a word where a letter
,
we get a word where a letter ![]() is after a letter
is after a letter ![]() .
In both cases we generate a word which is not in
.
In both cases we generate a word which is not in
![]() .height 5pt width 5pt depth 0pt
.height 5pt width 5pt depth 0pt
The generated language
PROOF.
These ![]() -producing agent-rules must
be in the form of
-producing agent-rules must
be in the form of
![]() but in this way we cannot guarantee that they are applied
at neighbouring positions,
thus we could also derive words with separated letters
but in this way we cannot guarantee that they are applied
at neighbouring positions,
thus we could also derive words with separated letters ![]() .height 5pt width 5pt depth 0pt
.height 5pt width 5pt depth 0pt
The consequence of the above lemmas is the following theorem: