



Next: Team behaviour in extended
Up: Team behaviour of simple
Previous: Team behaviour of simple
Contents
Definitions and previous
results in the non-extended case
The first team derivation mode which was studied for simple eco-grammar
systems is the derivation mode 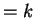 , where
in each step exactly
, where
in each step exactly  agents have to work.
agents have to work.
Definition 3.1
Consider a simple eco-grammar system
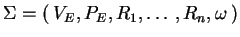
.
We say that
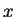
directly derives
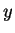
in
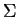
in derivation mode
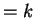
(with
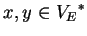
and
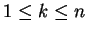
, written as
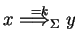
),
if
-
 , with
, with
 ,
,
 ,
,
 , and
, and
 ,
,
-
 , with
, with
 ,
,
 , and
, and
 ,
,
- there exist
 different agents in
different agents in 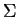 , namely
, namely
 , such that
, such that
 for
for
 , and
, and
-
 or
or
 ,
where
,
where
 is the
0L system of the environment.
is the
0L system of the environment.
We denote the transitive and reflexive closure of
 by
by
 .
The generated language consists of those words
which can be generated from the axiom in some derivation steps.
.
The generated language consists of those words
which can be generated from the axiom in some derivation steps.
Definition 3.2
Consider a simple eco-grammar system
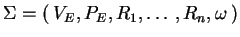
.
The generated language in the derivation mode
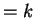
is the following:
In the following theorem,
we summarise the results
which are presented in [Csuhaj-Varjú and
KelemenováCsuhaj-Varjú and Kelemenová1998] and [CsimaCsima1997], where
relations between
language classes generated by simple eco-grammar systems
with different parameters  and
and  were examined. (The results
of [Csuhaj-Varjú and
KelemenováCsuhaj-Varjú and Kelemenová1998] are summarised and completed in [CsimaCsima1997].)
Let
were examined. (The results
of [Csuhaj-Varjú and
KelemenováCsuhaj-Varjú and Kelemenová1998] are summarised and completed in [CsimaCsima1997].)
Let
 denote the
class of languages generated by a simple EG system containing
denote the
class of languages generated by a simple EG system containing  agents and working in the derivation mode
agents and working in the derivation mode 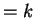 .
.




Next: Team behaviour in extended
Up: Team behaviour of simple
Previous: Team behaviour of simple
Contents
Csima Judit
2002-01-04
![]() , where
in each step exactly
, where
in each step exactly ![]() agents have to work.
agents have to work.
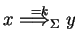 ),
if
),
if

![]() and
and ![]() were examined. (The results
of [Csuhaj-Varjú and
KelemenováCsuhaj-Varjú and Kelemenová1998] are summarised and completed in [CsimaCsima1997].)
Let
were examined. (The results
of [Csuhaj-Varjú and
KelemenováCsuhaj-Varjú and Kelemenová1998] are summarised and completed in [CsimaCsima1997].)
Let
![]() denote the
class of languages generated by a simple EG system containing
denote the
class of languages generated by a simple EG system containing ![]() agents and working in the derivation mode
agents and working in the derivation mode ![]() .
.