In the definition of a simple eco-grammar system the agents have context-free rules; now we modify this condition and we use new operations, insertion and replacement.
An insertion rule (an INS-type rule, for short) over an
alphabet ![]() is an ordered triple
is an ordered triple ![]() , where
, where
![]() .
We derive
.
We derive ![]() from
from ![]() by applying the insertion rule
by applying the insertion rule
![]() if
if
![]() ,
, ![]() , and
, and
![]() ,
,
![]() , with
, with
![]() .
.
By a replacement rule (a REP-type rule, for short) over
an alphabet ![]() we mean a rule in the form of
we mean a rule in the form of
![]() ,
where
,
where
![]() .
We derive
.
We derive ![]() from
from ![]() by the replacement rule
by the replacement rule
![]() if
if
![]() ,
,
![]() , and
, and
![]() .
.
By an insertion rule we can insert a new sub-word into the sentential
form, while by a replacement rule we can change only one letter.
We can see that there is also a difference between the context
restrictions in the two definitions. When applying an INS-type
rule, the two parts of the context condition, ![]() and
and ![]() ,
must be present in the sentential form in the
same order as presented in the rule, and the position of the insertion
can be anywhere between them.
In a REP-type rule the restriction is more strict: the close contexts
(that is, the neighbouring letters) are prescribed by
the rule.
This difference is motivated by the properties of DNA strands: local
point-mutations are determined by the close context of the position where the
mutation happens, while a global change in the DNA strand
(e.g. an insertion) is directed by the presence or absence of some
substrings in the strand.
,
must be present in the sentential form in the
same order as presented in the rule, and the position of the insertion
can be anywhere between them.
In a REP-type rule the restriction is more strict: the close contexts
(that is, the neighbouring letters) are prescribed by
the rule.
This difference is motivated by the properties of DNA strands: local
point-mutations are determined by the close context of the position where the
mutation happens, while a global change in the DNA strand
(e.g. an insertion) is directed by the presence or absence of some
substrings in the strand.
We study two different models using these new operations. The first type of models is the simple eco-grammar system of type INS or REP, where all the agents are of the same type. We study these systems in Section 4.2.
In the other model, in the hybrid eco-grammar system, there can be agents of both type.
We study different derivation modes in hybrid eco-grammar systems.
The difference lies in the restrictions prescribed for the
number of agents being active in a derivation step.
One of these possibilities is the derivation mode
![]() , defined below.
, defined below.
 ),
if
),
if

 ,
where
,
where
We emphasise the following consequences of the definition: more than
one agent can use the same context to apply an insertion
and the contexts of several replacements can be overlapping, too.
That is, for example in a sentential form
![]() (where the
(where the ![]() 's are letters) the following two insertion
rules and the following two replacement rules
can be used in the same derivation step:
's are letters) the following two insertion
rules and the following two replacement rules
can be used in the same derivation step:
![]() and
and
![]() ,
,
![]() , and
, and
![]() .
If the environment does not change the letters, with these four
rules we obtain either the word
.
If the environment does not change the letters, with these four
rules we obtain either the word
![]() or
the word
or
the word
![]() .
.
The above definition also implies that if we consider the derivation
mode
![]() in a hybrid EG system
in a hybrid EG system
![]() , then
, then
![]() ,
,
![]() and
and
![]() hold, where
hold, where ![]() is the number of INS-type agents in
the system.
is the number of INS-type agents in
the system.
In a derivation step
![]() we prescribe how many INS-type
and how many REP-type agents
work in a derivation step.
If we prescribe only the total number of agents working in a derivation step,
then we obtain derivation mode
we prescribe how many INS-type
and how many REP-type agents
work in a derivation step.
If we prescribe only the total number of agents working in a derivation step,
then we obtain derivation mode ![]() .
.
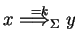 ),
if
),
if
 for some
for some
 and
and
 and
and


We present an example, which shows how a hybrid eco-grammar system works and which proves to be useful in the proofs of the chapter, too.
The parameters ![]() ,
, ![]() and
and ![]() in the notations
in the notations
![]() and
and
![]() refer to the following:
these languages are generated by a hybrid EG system defined in
Example 4.5, in the derivation mode
refer to the following:
these languages are generated by a hybrid EG system defined in
Example 4.5, in the derivation mode
![]() or
or ![]() .
The generating system contains
.
The generating system contains ![]() agents,
agents, ![]() agents of type INS,
agents of type INS,
![]() agents of type REP and the length of the axiom
is equal to
agents of type REP and the length of the axiom
is equal to ![]() , where
, where
![]() .
.
Having examined the system defined in Example 4.5
and the derivation process, we can see that
both generated languages,
![]() and
and
![]() , contain two types of words:
, contain two types of words: ![]() (the shortest word of this
type is the axiom,
(the shortest word of this
type is the axiom,
![]() ) and
) and
![]() , that is, words containing
the first
, that is, words containing
the first ![]() letters
letters ![]() and more
and more ![]() different letters
different letters ![]() ,
besides some letters
,
besides some letters ![]() .
In this latter type of words the symbols
.
In this latter type of words the symbols ![]() can stand anywhere except the
first and the last position of the word.
can stand anywhere except the
first and the last position of the word.
In the following we present some auxiliary statements which are used in the chapter. In these lemmas we use the following notions:
 or
or
 implies that
implies that
In this section, when applying this lemma to a language ![]() ,
the division
,
the division
![]() will be always straightforward, in general the letters of
alph
will be always straightforward, in general the letters of
alph![]() and
the letters of
alph
and
the letters of
alph![]() will be the letters with subscript
will be the letters with subscript ![]() and
and ![]() ,
respectively.
,
respectively.
PROOF.
First we prove a slightly weaker statement:
we show that there exists a positive integer ![]() , such that
for
, such that
for ![]() if
if ![]() ,
, ![]() , and
, and
 or
or
 ,
then
,
then ![]() and
and ![]() .
That is, first we show that words over one of the sub-alphabets and
being longer than
.
That is, first we show that words over one of the sub-alphabets and
being longer than ![]() can be derived only from words
being over the other sub-alphabet.
can be derived only from words
being over the other sub-alphabet.
Let us define ![]() as follows:
as follows:
 or
or
 ,
,
Since ![]() , it is sure that in the step
, it is sure that in the step
 or
or
 the system
the system ![]() uses at least one production in the form of
uses at least one production in the form of
![]() from
from ![]() , where
, where
![]() alph
alph![]() is a letter with unbounded
occurrence and
is a letter with unbounded
occurrence and
![]() is a non-empty word being
over
alph
is a non-empty word being
over
alph![]() (otherwise
(otherwise ![]() would hold because of the definition of
would hold because of the definition of
![]() ).
).
The existence of such a rule implies that
![]() cannot perform any derivation step
cannot perform any derivation step
 or
or
 ,
where
,
where
![]() and
and
![]() ,
, ![]() , that is,
such a derivation step
where from a
word over
alph
, that is,
such a derivation step
where from a
word over
alph![]() a non-empty word over the other sub-alphabet would
be derived.
This is true because in this case,
by combining the above rule
a non-empty word over the other sub-alphabet would
be derived.
This is true because in this case,
by combining the above rule
![]() of
of ![]() and the rules used
in the step
and the rules used
in the step
 or
or
 ,
we would be able to derive words
in which letters from both sub-alphabets occur.
(Here we use condition (ii),
which guarantees that there is a word in
,
we would be able to derive words
in which letters from both sub-alphabets occur.
(Here we use condition (ii),
which guarantees that there is a word in ![]() in which
in which
![]() is a sub-word and
is a sub-word and ![]() occurs at least once.)
occurs at least once.)
Therefore the words over
alph![]() can be
derived only from words over the same sub-alphabet, which is
also true for those words over
alph
can be
derived only from words over the same sub-alphabet, which is
also true for those words over
alph![]() which are longer than
which are longer than ![]() .
Since we know that such words exist
(
.
Since we know that such words exist
(![]() is an infinite language) we can conclude that there exists
a rule in
is an infinite language) we can conclude that there exists
a rule in ![]() in the form of
in the form of
![]() , where
, where
![]() alph
alph![]() is a letter with unbounded occurrence and
is a letter with unbounded occurrence and
![]() .
.
The existence of such a rule implies that
![]() cannot perform any derivation step
where from a word over
alph
cannot perform any derivation step
where from a word over
alph![]() a non-empty word over the other
sub-alphabet
alph
a non-empty word over the other
sub-alphabet
alph![]() would
be derived because
in this case, combining this derivation step with the application of the
above rule
would
be derived because
in this case, combining this derivation step with the application of the
above rule
![]() ,
we could generate words in which letters from both sub-alphabets occur.
,
we could generate words in which letters from both sub-alphabets occur.
Hence we have obtained
that words over one of the sub-alphabets can be derived only
from words over this sub-alphabet, which is a contradiction because
in this way only the words of ![]() or only the words of
or only the words of ![]() could be
derived, depending on the alphabet of the axiom.
could be
derived, depending on the alphabet of the axiom.
Thus we have proved that words longer than ![]() being over one of the
sub-alphabets can be derived only from words being over the other sub-alphabet.
being over one of the
sub-alphabets can be derived only from words being over the other sub-alphabet.
Now we prove the statement of the lemma.
Let us suppose that there exists a derivation step
 or
or
 ,
such that
,
such that
![]() .
Since we have seen that sufficiently long words over
alph
.
Since we have seen that sufficiently long words over
alph![]() can be derived only from words over
alph
can be derived only from words over
alph![]() and
since
and
since ![]() and
and ![]() are infinite languages,
there must be at least one rule in
are infinite languages,
there must be at least one rule in ![]() in the form of
in the form of
![]() ,
where
,
where
![]() alph
alph![]() is a letter with unbounded occurrence,
is a letter with unbounded occurrence,
![]() and
and ![]() .
Combining this rule with the derivation step
.
Combining this rule with the derivation step
 or
or
 ,
we could derive words in which symbols from both sub-alphabets occur.height 5pt width 5pt depth 0pt
,
we could derive words in which symbols from both sub-alphabets occur.height 5pt width 5pt depth 0pt
In Section 4.2 we use a modified version of the above
lemma for simple eco-grammar systems of type CF.
 imply that
imply that
PROOF.
To complete the proof,
we show that the inclusion is proper if ![]() .
.
![]() (see Example 4.5) has the properties
required by Lemma 4.9 if
(see Example 4.5) has the properties
required by Lemma 4.9 if ![]() , thus the lemma proves that it
cannot be generated by
a hybrid eco-grammar system containing less than
, thus the lemma proves that it
cannot be generated by
a hybrid eco-grammar system containing less than ![]() agents.
agents.
![]()
It follows from the above proof that
![]() .
The following example shows that the inclusion is proper.
.
The following example shows that the inclusion is proper.
Let
![]() be the following hybrid eco-grammar system:
be the following hybrid eco-grammar system:


Let us suppose that
![]() with a
hybrid eco-grammar system
with a
hybrid eco-grammar system
![]() containing only one agent.
containing only one agent.
We can apply Lemma 4.7 to
![]() ,
with
,
with
![]() ,
,
![]() ,
therefore words containing
letters
,
therefore words containing
letters ![]() or
or ![]() must be derived in
must be derived in
![]() from words
in the form of
from words
in the form of
![]() .
.
By the rules of
![]() we cannot introduce
letters
we cannot introduce
letters ![]() or
or ![]() because in this case
the number of letters
because in this case
the number of letters ![]() or
or ![]() would not be bounded
in the generated words.
would not be bounded
in the generated words.
If
![]() and
and
![]() are rules of
are rules of
![]() , then
, then
![]() and
and
![]() ,
otherwise words with mixed occurrences of letters
,
otherwise words with mixed occurrences of letters ![]() and
and ![]() or
words starting with
or
words starting with
![]() or ending with
or ending with ![]() would be in the generated language.
Moreover,
there must be at least one rule in
would be in the generated language.
Moreover,
there must be at least one rule in
![]() in the form of
in the form of
![]() and
and
![]() with
with
![]() and
and
![]() ,
otherwise
,
otherwise ![]() or
or ![]() would be letters with
bounded occurrence, which is not the case.
would be letters with
bounded occurrence, which is not the case.
The only possibility to generate words with a sub-word
![]() is to use insertion
rules because neither
is to use insertion
rules because neither
![]() nor a replacement rule can generate it.
In
nor a replacement rule can generate it.
In
![]() there is only one agent
and so this agent must be an INS-type one,
that is, the
letter
there is only one agent
and so this agent must be an INS-type one,
that is, the
letter ![]() is also generated by an insertion rule.
This rule is in the form of
is also generated by an insertion rule.
This rule is in the form of
![]() ,
,
![]() ,
,
![]() ,
,
![]() , or
, or
![]() ,
where
,
where
![]() and
and
![]() .
But none of these insertion rules is able to determine the exact position of
the letter
.
But none of these insertion rules is able to determine the exact position of
the letter ![]() : using the non-erasing
rules of
: using the non-erasing
rules of
![]() , we could generate words
where the letter
, we could generate words
where the letter ![]() occurs
at a wrong position, in the middle of a sequence of letters
occurs
at a wrong position, in the middle of a sequence of letters ![]() or
or ![]() .
.
![]()
We have to prove that
![]() if
if
![]() , since the other direction follows from the proof of part 1.
, since the other direction follows from the proof of part 1.
Let us suppose that
![]() with a hybrid eco-grammar system
with a hybrid eco-grammar system
![]() . Then let
. Then let
![]() be the following system:
be the following system:
If
![]() , then
, then
![]() holds by Lemma 4.9
(for the definition of the language
holds by Lemma 4.9
(for the definition of the language
![]() see Example 4.5).
see Example 4.5).
On the other hand, first we deal with the case
![]() and we
prove that
and we
prove that
![]() if
if
![]() .
First we show that if
.
First we show that if
![]() with a
hybrid eco-grammar system
with a
hybrid eco-grammar system
![]() , then
, then ![]() does not contain the rule
does not contain the rule
![]() .
.
If ![]() has this rule, then the REP-type agents could
not introduce letters
has this rule, then the REP-type agents could
not introduce letters ![]() , since by using a
replacement rule which introduce a
letter
, since by using a
replacement rule which introduce a
letter ![]() and the erasing rule of
and the erasing rule of ![]() for all letters preceding the first letter
for all letters preceding the first letter ![]() , we would generate a word
whose first symbol is a letter
, we would generate a word
whose first symbol is a letter ![]() .
(Here we use that Lemma 4.7 can be applied for
.
(Here we use that Lemma 4.7 can be applied for
![]() with
with
![]() and hence words containing letters
and hence words containing letters ![]() can be
derived only from
words being over
can be
derived only from
words being over
![]() ).
).
Because of the same reason,
all insertion rules introducing a letter ![]() must be in the form
must be in the form
![]() (with
(with
![]() ,
,
![]() ), so that
we could avoid the letters
), so that
we could avoid the letters
![]() as the first or as the last symbol of the words.
as the first or as the last symbol of the words.
Since the environment cannot introduce letters ![]() (
(![]() is a letter with
unbounded occurrence), the only possibility
to introduce them is to use these insertion rules.
But with these rules we cannot introduce sub-words
is a letter with
unbounded occurrence), the only possibility
to introduce them is to use these insertion rules.
But with these rules we cannot introduce sub-words ![]() ,
which is a contradiction.
(It is not possible either to produce these sub-words by
one agent; we can see this
by using the same idea as the one used in Lemma 4.9.)
Thus we have proved that
,
which is a contradiction.
(It is not possible either to produce these sub-words by
one agent; we can see this
by using the same idea as the one used in Lemma 4.9.)
Thus we have proved that
![]() is not a possible rule in
is not a possible rule in ![]() .
.
In
![]() the shortest word containing letters
the shortest word containing letters ![]() is
in the form of
is
in the form of
![]() .
This word must be derived in
.
This word must be derived in ![]() from the word
from the word
![]() because this is
the only shorter word in the set
because this is
the only shorter word in the set
![]() (here we use again
the fact that we can apply Lemma 4.7
to the language
(here we use again
the fact that we can apply Lemma 4.7
to the language
![]() ).
).
We know that ![]() cannot use erasing rule during this step
and we also know that REP-type agents cannot perform any
actions on
cannot use erasing rule during this step
and we also know that REP-type agents cannot perform any
actions on ![]() because it contains only two symbols.
It means that in this step at most
because it contains only two symbols.
It means that in this step at most ![]() (INS-type) agents can work,
that is,
(INS-type) agents can work,
that is,
![]() , which is a contradiction because we supposed that
, which is a contradiction because we supposed that ![]() .
.
To complete the proof, we show that
if ![]() , then
, then
![]() .
.
It is clear that ![]() can be generated by the following hybrid
EG system
can be generated by the following hybrid
EG system
![]() in mode
in mode ![]() :
:
PROOF.
First we consider the case when
![]() .
Applying Lemma 4.9 to
.
Applying Lemma 4.9 to
![]() (see Example 4.5), we obtain that
if
(see Example 4.5), we obtain that
if
![]() with a
hybrid
eco-grammar system
with a
hybrid
eco-grammar system
![]()
![]() , then
, then
![]() .
Since
.
Since
![]() , we can use the same idea as in part 4
of Theorem 4.10 and we can conclude that
, we can use the same idea as in part 4
of Theorem 4.10 and we can conclude that ![]() cannot contain
the rule
cannot contain
the rule
![]() .
Using this fact and
examining the rules used in the derivation step
.
Using this fact and
examining the rules used in the derivation step
![$ {a_1}^{k_2+2}\ensuremath{\stackrel{(={\ell}_1,={\ell}_2)}{{\Longrightarrow}_{\Sigma}}}{a_2}
{[c_1,\ldots,c_{k_1},c_{i_1},c_{i_2},\ldots,c_{i_{k_2}}]}^Pa_2$](img656.gif) (which is the only possibility to derive the latter word in
(which is the only possibility to derive the latter word in ![]() )
we obtain that
)
we obtain that
![]() and
and
![]() .
Since
.
Since
![]() , we have
, we have
![]() and
and
![]() .
This gives that
.
This gives that
![]() , if
, if
![]() and
and
![]() or
or
![]() .
.
For completing the proof, we construct
two languages which show the incomparability when
![]() .
.
In the case ![]() =1,
=1, ![]()
![]() holds if
holds if
![]() or
or
![]() by the same reason as
in part 4 of Theorem 4.10.
by the same reason as
in part 4 of Theorem 4.10.
In the other case, that is, when ![]() =0 and
=0 and ![]() =
=![]() ,
the language generated by the
following hybrid EG system
,
the language generated by the
following hybrid EG system ![]() in mode
in mode ![]() shows the incomparability: this language cannot
be generated by hybrid EG systems in mode
shows the incomparability: this language cannot
be generated by hybrid EG systems in mode
![]() if
if
![]() or
or
![]() .
.
Let
![]() be the following hybrid EG system:
be the following hybrid EG system:
![]() cannot introduce the letter
cannot introduce the letter ![]() ,
because in this case more than
one letters
,
because in this case more than
one letters ![]() would be in some words (since
would be in some words (since ![]() and
and ![]() are letters with
unbounded occurrence).
Moreover, for all the rules
are letters with
unbounded occurrence).
Moreover, for all the rules
![]() and
and
![]() of
of
![]()
![]() and
and
![]() hold, otherwise
words with mixed letters
hold, otherwise
words with mixed letters ![]() and
and ![]() or words starting
with a letter
or words starting
with a letter ![]() or ending with a letter
or ending with a letter ![]() would be in the generated language.
would be in the generated language.
![]() cannot contain rules in the form of
cannot contain rules in the form of
![]() or
or
![]() because in this case the
number of letters
because in this case the
number of letters ![]() or
or ![]() would be bounded in the generated words.
Similarly, for all rules
would be bounded in the generated words.
Similarly, for all rules
![]() or
or
![]() of
of
![]()
![]() and
and
![]() must hold and
must hold and
![]() cannot
contain the rules
cannot
contain the rules
![]() and
and
![]() .
.
Since
![]() cannot contain erasing rules, the only possibility
to derive the word
cannot contain erasing rules, the only possibility
to derive the word
![]() is
the derivation step
is
the derivation step
![]() .
.
Considering the lengths of these two words, there are five possibilities
for
![]() :
:
In case 5 the replacement rule used in the derivation step
must be
![]() . (The letter
. (The letter
![]() cannot be introduced by insertion because
in this case we could not determine the exact position of it.)
It is also sure that we have to use the rule
cannot be introduced by insertion because
in this case we could not determine the exact position of it.)
It is also sure that we have to use the rule
![]() or
or
![]() for introducing a letter
for introducing a letter ![]() .
But with this last insertion rule we could also insert a letter
.
But with this last insertion rule we could also insert a letter ![]() in the middle of a
sequence of letters
in the middle of a
sequence of letters ![]() , which is a contradiction.
, which is a contradiction.
In case 3 when
![]() , we have two possibilities for
the rules in the derivation step
, we have two possibilities for
the rules in the derivation step
![]() .
The letter
.
The letter ![]() is introduced by a replacement and
either
the environment uses the rule
is introduced by a replacement and
either
the environment uses the rule
![]() and
one INS-type agent introduces a
and
one INS-type agent introduces a ![]() by a rule of type
by a rule of type
![]() ,
,
![]() or
the environment uses the rule
or
the environment uses the rule
![]() and
one INS-type agent uses the rule
and
one INS-type agent uses the rule
![]() ,
,
![]() , or
, or
![]() .
.
The first case is not possible because of the same reason as in case 5.
The second case implies that
![]() is the only rule in
is the only rule in
![]() to rewrite
to rewrite ![]() , otherwise more then one word
in the form of
, otherwise more then one word
in the form of
![]() could be generated.
But in this case for all derivation steps
could be generated.
But in this case for all derivation steps
![]() the
difference
the
difference
![]() would be bounded, which is impossible.
Thus the only possibility is
would be bounded, which is impossible.
Thus the only possibility is
![]() . height 5pt width 5pt depth 0pt
. height 5pt width 5pt depth 0pt
Finally, we show that hybrid EG
systems are more powerful than homogeneous INS- or
REP-type systems.