In an extended simple eco-grammar system we distinguish a subset of the alphabet, and only words over this terminal alphabet are in the generated language.
The definition of the derivation mode ![]() is the same as in
Definition 3.1, the difference lies in the definition of the
generated language.
is the same as in
Definition 3.1, the difference lies in the definition of the
generated language.
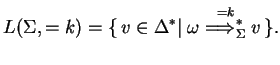
In this section
we study extended simple eco-grammar systems with or without
![]() -rules.
When we allow
-rules.
When we allow ![]() -rules
in
-rules
in ![]() and in the sets
and in the sets ![]() , we use the following notations:
the class of languages generated by
extended simple eco-grammar systems is denoted by
, we use the following notations:
the class of languages generated by
extended simple eco-grammar systems is denoted by
![]() (in this notation the first
(in this notation the first ![]() means ``extended'',
the second one refers to ``eco'');
the class of languages generated by systems containing
means ``extended'',
the second one refers to ``eco'');
the class of languages generated by systems containing
![]() agents and
operating in the derivation mode
agents and
operating in the derivation mode ![]() is denoted by
is denoted by
![]() .
We omit the notation
.
We omit the notation
![]() if
if ![]() -rules are not allowed neither in
-rules are not allowed neither in
![]() nor in the sets
nor in the sets ![]() :
:
![]() and
and
![]() .
.
We present results about the hierarchy
of language classes generated by ![]() agents in the derivation mode
agents in the derivation mode ![]() .
Most of the statements and proofs are true with or without
.
Most of the statements and proofs are true with or without
![]() -rules, this fact is denoted by the superscript
-rules, this fact is denoted by the superscript ![]() ;
sometimes a statement
is true only when
;
sometimes a statement
is true only when ![]() -rules are allowed, in this case we will
emhasize this fact.
-rules are allowed, in this case we will
emhasize this fact.
First we examine the role of the first parameter: the number of agents.
PROOF.
PROOF.
Let
![]() be the following system:
be the following system:
In
![]() , the set
, the set ![]() is included in the set of rules
of each agent
in the form of
is included in the set of rules
of each agent
in the form of
![]() .
When an agent uses a rule corresponding
to
.
When an agent uses a rule corresponding
to ![]() ,
a primed letter is introduced as well.
The only agent which is able to make these primed letters disappear is
,
a primed letter is introduced as well.
The only agent which is able to make these primed letters disappear is
![]() ; this construction guarantees (considering the
rules of
; this construction guarantees (considering the
rules of
![]() ) that the derivation
cannot terminate with a terminal word if the agents
use more than one rule from
) that the derivation
cannot terminate with a terminal word if the agents
use more than one rule from
![]() at
the same derivation step.
at
the same derivation step.
If in a derivation step of ![]() the agents
the agents
![]() work and
work and ![]() for
for
![]() , then the simulation
goes as follows.
, then the simulation
goes as follows.
In the first simulation step in
![]() the agents
the agents
![]() work using rules from
work using rules from
![]() , corresponding to the step of
, corresponding to the step of ![]() .
Then the environment uses the same rules as in
.
Then the environment uses the same rules as in ![]() (in the form
of
(in the form
of
![]() ).
).
In the second simulation step the agents
![]() rewrite
rewrite ![]() letters and
the environment rewrites the remaining letters by using the rules
in the form of
letters and
the environment rewrites the remaining letters by using the rules
in the form of
![]() . (There are at least
. (There are at least ![]() letters
in the sentential form because there are no
letters
in the sentential form because there are no ![]() -rules in
-rules in ![]() .)
.)
If ![]() was among the agents
was among the agents
![]() in a derivation step in
in a derivation step in ![]() , then the two simulation steps of
, then the two simulation steps of
![]() are the following.
are the following.
In the first simulation step we choose one agent
![]() in
in
![]() , such that
, such that
![]() for any
for any
![]() .
This is possible because
.
This is possible because ![]() .
This agent simulates the work of
.
This agent simulates the work of ![]() by using
the corresponding rule of
by using
the corresponding rule of
![]() .
.
The agents
![]() simulate the other
rules of the agents and
the environment rewrites the remaining letters in the same way as in
simulate the other
rules of the agents and
the environment rewrites the remaining letters in the same way as in
![]() .
.
In the second simulation step
![]() rewrites the primed letter,
other
rewrites the primed letter,
other ![]() agents rewrite
agents rewrite ![]() other letters and the
environment rewrites
the remaining letters into symbols of
other letters and the
environment rewrites
the remaining letters into symbols of ![]() .
.
Since we can simulate every derivation step of ![]() by a derivation
sequence of
by a derivation
sequence of
![]() , we obtain
, we obtain
![]() .
.
On the other hand, for any
derivation sequence of
![]() resulting in a terminal word, there exists
a derivation in
resulting in a terminal word, there exists
a derivation in ![]() generating the same word, which gives the other
inclusion
generating the same word, which gives the other
inclusion
![]() .
We will simulate two derivation steps of these sequences of
.
We will simulate two derivation steps of these sequences of
![]() by one step of
by one step of ![]() .
For each
.
For each
![]() (which implies
(which implies
![]() because
because ![]() -rules
are not allowed)
there exists a derivation sequence in
-rules
are not allowed)
there exists a derivation sequence in
![]() in the form of
in the form of
Considering the rules in
![]() , it is easy to see
that there can be at most one primed letter in the
previous word
, it is easy to see
that there can be at most one primed letter in the
previous word ![]() .
.
The fact that there is no primed letter in ![]() means that in the
means that in the ![]() th step
th step ![]() agents,
agents,
![]() , use
rules from the sets
, use
rules from the sets
![]() with
with
![]() .
In this case we can simulate the last two derivation
steps of
.
In this case we can simulate the last two derivation
steps of
![]() by one derivation step of
by one derivation step of
![]() , using the corresponding rules of the
agents
, using the corresponding rules of the
agents
![]() and the environment.
and the environment.
The other possibility gives that ![]() agents,
agents,
![]() , use
rules from the sets
, use
rules from the sets
![]() with
with
![]() and
one agent uses a rule of
and
one agent uses a rule of
![]() .
Then we can simulate the last two steps by one step in
.
Then we can simulate the last two steps by one step in ![]() when
the agents
when
the agents
![]() and the environment
use the corresponding rules.
and the environment
use the corresponding rules.
In both cases
![]() , thus we
can continue the simulation by giving the role of
, thus we
can continue the simulation by giving the role of ![]() to
to ![]() .
Since the axiom is over
.
Since the axiom is over ![]() and
and ![]() is an even number
(see the rules of
is an even number
(see the rules of
![]() ), it can be proved by induction on the length
of the derivation that we can simulate the whole derivation sequence.
), it can be proved by induction on the length
of the derivation that we can simulate the whole derivation sequence.
With ![]() -rules
-rules
The main idea is the same as it was in the ![]() -free case:
we show that we can simulate any extended
simple EG system
-free case:
we show that we can simulate any extended
simple EG system
![]() working in the derivation mode
working in the derivation mode ![]() by another extended simple EG system
by another extended simple EG system
![]() working also in the derivation mode
working also in the derivation mode ![]() .
.
Let
![]() be the following system:
be the following system:
Now we turn our attention to the second parameter: the number of agents working in a derivation step. Considering Corollary 3.7, it is enough to examine the relations of language classes
For the ![]() -free case, it was proved in [Dassow and MihalacheDassow and
Mihalache1995] that
-free case, it was proved in [Dassow and MihalacheDassow and
Mihalache1995] that
![]() is included in
is included in
![]() .
In the following lemma we present the same result for extended simple
EG systems
with
.
In the following lemma we present the same result for extended simple
EG systems
with ![]() -rules as well.
We give a simulation which is based on the construction
used in [Dassow and MihalacheDassow and
Mihalache1995],
hence in the first part of our proof
we briefly summarise their construction and their explanation
for the
-rules as well.
We give a simulation which is based on the construction
used in [Dassow and MihalacheDassow and
Mihalache1995],
hence in the first part of our proof
we briefly summarise their construction and their explanation
for the ![]() -free case.
Then in the second part of the proof we give the modifications
which are necessary to obtain the same result when
-free case.
Then in the second part of the proof we give the modifications
which are necessary to obtain the same result when ![]() -rules are
allowed.
-rules are
allowed.
PROOF.
Let
![]() be the following:
be the following:
Let
It follows from the construction that the environment cannot
introduce two barred letters, because in this case the derivation would never
result in a terminal word because of the symbol ![]() .
Therefore, only the sequences consisting of pairs of steps
of this type can derive terminal words in
.
Therefore, only the sequences consisting of pairs of steps
of this type can derive terminal words in
![]() ,
but these derivations
can be performed in
,
but these derivations
can be performed in ![]() as well.
as well.
In the case when ![]() -rules are allowed we have to modify the above
construction in the following way.
-rules are allowed we have to modify the above
construction in the following way.
PROOF.
Now we show that
![]() .
For any
.
For any
![]() there is a derivation in
there is a derivation in
![]() in the form
in the form

PROOF.
Using this fact together with Lemma 3.8 and Lemma 3.10,
we can present the result of the
![]() -free case in the following theorem.
-free case in the following theorem.
We summarise the results of this section in the form of a diagram, where
a straight arrow indicates a proper inclusion;
the class the arrow leaves is included in the class the arrow points at.
The inclusion
![]() can be proved
by any language of
can be proved
by any language of
![]() containing the empty word,
containing the empty word,
![]() .
.
We use the notation ![]() for
for ![]() , where
, where ![]() denotes an
arbitrary positive integer, such that
denotes an
arbitrary positive integer, such that ![]() .
.