Enlightened landscape

Consider a landscape composed of connected line segments:

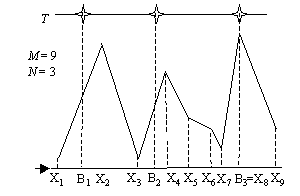
Above the landscape, N light bulbs are hang at the same height T in various horizontal positions. The purpose of these light bulbs is to light up the entire landscape. A landscape point is considered lit if it can "see" a light bulb directly, that is, if the line segment which links the point with a bulb does not contain any other landscape segments point.

Task
Write a program that determines the mi-ni-mum number of light bulbs that must be switched on in order to illuminate the entire landscape.

Input
Input file name: LIGHT.IN
Line 1: M

An integer, the number of landscape height specifications, including the first and the last point of the landscape.
Lines 2..M+1: X_i H_i

Two integers, separated by a space: the landscape height H_i at horizontal position X_i, 1 <= i <= M; for 1 <= i <= M-1 we have X_i+1 > X_i; any two consecutive specified points identify a segment of line in the landscape.
Line M+2: N T

Two integers, separated by a space, the num-ber of light bulbs and their height coordinate (altitude). The bulbs are numbered from 1 to N)
Line M+3: B₁ B₂ ... B_N

N integers, separated by spaces: the hori-zon-tal coordinates of the light bulbs Bi+1 > Bi, 1 <= i <=N-1;

Output
File name: LIGHT.OUT
Line 1: K

An integer: the minimum number of light bulbs to be switched on.
Line 2: L₁ L₂ ... L_K

K integers, separated by spaces: the labels of the light bulbs to be switched on spe-cified in increasing order of their horizontal coordinates.

Limits

1 <= M <= 200

1 <= N <= 200

1 <= X_i <= 10000 for 1 <= i <= M

1 < T <= 10000

1 <= H_i <= 10000 for 1 <= i <= M

T > H_i for any 1 <= i <= M

X₁ <= B₁ and B_N <= X_M

The task always has a solution for the test data. If there are multiple solutions, only one is required.

Example

LIGHT.IN          LIGHT.OUT 
6                 2
1 1               1 4
3 3
4 1
7 1
8 3
11 1
4 5
1 5 6 10