


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
9. feladatsor (2002. ápr. 19.)
- Határozd meg tetszőleges
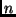 pozitív egész számra
pozitív egész számra
- az
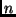 -edik komplex egységgyökök összegét;
-edik komplex egységgyökök összegét;
- az
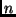 -edik komplex egységgyökök szorzatát!
-edik komplex egységgyökök szorzatát!
- Határozd meg az alábbi halmazok számosságát:
- 0 és 1 közötti racionális számok halmaza;
- 0 és 1 közötti irracionális számok halmaza;
- a sík azon pontjainak halmaza, melyeknek mindkét koordinátája egész;
- a tér azon pontjainak halmaza, melyeknek mindhárom koordinátája
racionális;
- a tér azon pontjának halmaza, melyeknek
 és
és 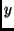 koordinátája egész,
koordinátája egész,  koorditátja pedig irracionális!
koorditátja pedig irracionális!
- Mi a számossága annak a halmaznak, melynek elemei azok a számok, melyek
felírhatók
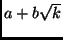 alakban, ahol
alakban, ahol 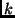 pozitív egész,
pozitív egész, 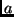 és
és 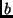 pedig racionális
számok? (ZH. 1999. dec.)
pedig racionális
számok? (ZH. 1999. dec.)
- Mi a valós számegyenesen megadható olyan nyílt intervallumok halmazának
számossága, melyeknek mindkét végpontja racionális szám? (Vizsga, 1999. febr.)
- Hányféleképpen lehet kiszínezni a természetes számokat
- két színnel;
- négy színnel úgy, hogy a színezés periodikus legyen; (A színezés
periodikus, ha van olyan
 szám - periódus, melyre
szám - periódus, melyre 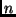 és
és 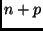 szám színe
mindig ugyanaz.)
szám színe
mindig ugyanaz.)
- két színnel - pirossal és kékkel - úgy, hogy az első
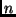 szám között több
a kék, mint a piros minden
szám között több
a kék, mint a piros minden 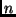 esetén;
esetén;
- három színnel úgy, hogy a szomszédos számok különböző színűek?
- Mennyi az olyan 0-val kezdődő végtelen hosszú egész tagú sorozatok halmazának
számossága, melyekben bármely két szomszédos tag különbsége 1 vagy -1? (Vizsga,
2001. jan.)
- Bontsuk a sík összes egyeneseinek halmazát két részhalmazra:
 -et alkossák
az origón átmenő egyenesek,
-et alkossák
az origón átmenő egyenesek, 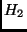 -t a többi egyenes. Határozzuk meg
-t a többi egyenes. Határozzuk meg  és
és 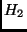 számosságát! (ZH. 2000. dec.)
számosságát! (ZH. 2000. dec.)
- Hány olyan végtelen hosszú
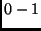 sorozat van, amiben az 1-esek száma
véges
?
(Vizsga, 1999. jan.)
sorozat van, amiben az 1-esek száma
véges
?
(Vizsga, 1999. jan.)



Next: About this document ...
Veto Balint
2002-04-16
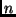 -edik komplex egységgyökök összegét;
-edik komplex egységgyökök összegét;
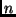 -edik komplex egységgyökök szorzatát!
-edik komplex egységgyökök szorzatát!
 és
és 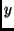 koordinátája egész,
koordinátája egész,  koorditátja pedig irracionális!
koorditátja pedig irracionális!
 szám - periódus, melyre
szám - periódus, melyre 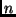 és
és 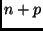 szám színe
mindig ugyanaz.)
szám színe
mindig ugyanaz.)
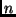 szám között több
a kék, mint a piros minden
szám között több
a kék, mint a piros minden 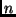 esetén;
esetén;