


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
7. feladatsor (2002. ápr. 5.)
- Legyen
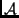 lineáris leképezés
lineáris leképezés 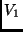 -ről
-ről 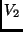 -be,
-be,
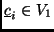 .
Melyek igazak az alábbi állítások közül?
.
Melyek igazak az alábbi állítások közül?
- Ha
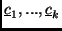 generátorrendszer
generátorrendszer 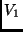 -ben, akkor
-ben, akkor
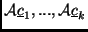 generátorrendszer
generátorrendszer 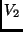 -ben.
-ben.
- Ha
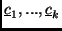 generátorrendszer
generátorrendszer 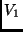 -ben, akkor
-ben, akkor
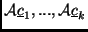 generátorrendszer Im
generátorrendszer Im
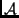 -ban.
-ban.
- Ha
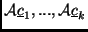 generátorrendszer Im
generátorrendszer Im
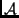 -ban, akkor
-ban, akkor
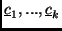 generátorrendszer
generátorrendszer 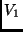 -ben.
-ben.
- Ha
 , akkor
, akkor
 .
.
- Az
 lineáris leképezésről a következőket tudjuk:
lineáris leképezésről a következőket tudjuk:
- Bármely 4 elem képe lineárisan összefüggő.
- Bármely 6 lineárisan független
 -beli elem között van olyan,
amelyiknek a képe nem a nulla.
-beli elem között van olyan,
amelyiknek a képe nem a nulla.
Bizonyítsd be, hogy
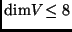 !
!
- Végezd el az alábbi műveleteket a komlex számok halmazán!
- Legyen
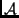 olyan lineáris transzformáció, melyre
olyan lineáris transzformáció, melyre
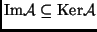 . Bizonyítsuk be, hogy az
. Bizonyítsuk be, hogy az
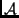 transzformáció (tetszőleges bázisban felírt)
transzformáció (tetszőleges bázisban felírt) 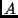 mátrixára
mátrixára  .
(ZH. 1997. nov.)
.
(ZH. 1997. nov.)
- Legyen
 a síkvektorok szokásos vektortere,
a síkvektorok szokásos vektortere,
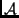 és
és
 pedig
pedig
 egy-egy lineáris transzformációja. Döntsük el, hogy
egy-egy lineáris transzformációja. Döntsük el, hogy
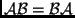 teljesül-e, ha
teljesül-e, ha
-
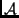 az
az  tengelyre,
tengelyre,
 az
az 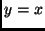 egyenesre történő tükrözés.
egyenesre történő tükrözés.
-
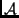 az origó körüli
az origó körüli
 -os,
-os,
 az origó körüli
az origó körüli
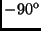 -os elforgatás.
-os elforgatás.
-
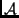 az origóból történő ötszörös nagyítás,
az origóból történő ötszörös nagyítás,
 az origó körüli
az origó körüli
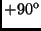 -os elforgatás.
-os elforgatás.
- Az
 lineáris transzformációt tükrözésnek nevezzük,
ha minden
lineáris transzformációt tükrözésnek nevezzük,
ha minden
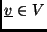 vektorra teljesül
vektorra teljesül
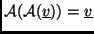 .
Bizonyítsuk be, hogy a tükrözés mátrixának a determinánsa nem lehet
0. (ZH. 2000. dec.)
.
Bizonyítsuk be, hogy a tükrözés mátrixának a determinánsa nem lehet
0. (ZH. 2000. dec.)



Next: About this document ...
Veto Balint
2002-04-03
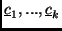 generátorrendszer
generátorrendszer 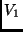 -ben, akkor
-ben, akkor
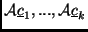 generátorrendszer
generátorrendszer 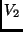 -ben.
-ben.
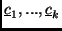 generátorrendszer
generátorrendszer 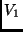 -ben, akkor
-ben, akkor
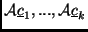 generátorrendszer Im
generátorrendszer Im
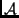 -ban.
-ban.
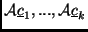 generátorrendszer Im
generátorrendszer Im
 -ban, akkor
-ban, akkor
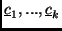 generátorrendszer
generátorrendszer 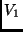 -ben.
-ben.
 , akkor
, akkor
 .
.
 -beli elem között van olyan,
amelyiknek a képe nem a nulla.
-beli elem között van olyan,
amelyiknek a képe nem a nulla.
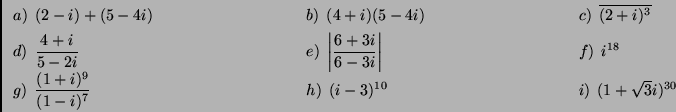
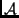 az
az  tengelyre,
tengelyre,
 az
az 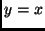 egyenesre történő tükrözés.
egyenesre történő tükrözés.
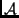 az origó körüli
az origó körüli
 -os,
-os,
 az origó körüli
az origó körüli
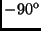 -os elforgatás.
-os elforgatás.
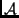 az origóból történő ötszörös nagyítás,
az origóból történő ötszörös nagyítás,
 az origó körüli
az origó körüli
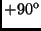 -os elforgatás.
-os elforgatás.