


Next: About this document ...
Bevezetés a számításelméletbe 1. gyakorlat
1. feladatsor (2002. febr. 15.)
- Írjuk fel annak a síknak az egyenletét, amely párhuzamos a
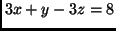 egyenletű síkkal, és átmegy a
egyenletű síkkal, és átmegy a 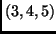 ponton, ill.
amelyik átmegy az origón!
ponton, ill.
amelyik átmegy az origón!
- Határozd meg az
 és a
és a 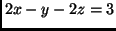 egyenletű síkok
metszésvonalának azt a pontját, amelyik az
egyenletű síkok
metszésvonalának azt a pontját, amelyik az 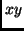 síkba
(
síkba
( és
és  tengelyek által meghatározott síkba) esik!
(ZH. 1999. nov.)
tengelyek által meghatározott síkba) esik!
(ZH. 1999. nov.)
- Az
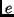 egyenes egyenlete
egyenes egyenlete
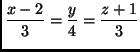 .
Írd fel az irányvektorát! Ennek segítségével határozd meg annak az egyenesnek
az egyenletrendszerét kétféleképpen (paraméteresen is), amely párhuzamos
.
Írd fel az irányvektorát! Ennek segítségével határozd meg annak az egyenesnek
az egyenletrendszerét kétféleképpen (paraméteresen is), amely párhuzamos
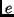 -vel, és áthalad a
-vel, és áthalad a  ponton!
ponton!
- Számítsd ki az
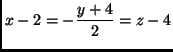 , és
, és
 egyenesek metszésponját!
egyenesek metszésponját!
- Határozzuk meg a háromdimenziós térben az
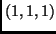 és a
és a 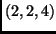 pontokon átmenő egyenesnek és a
pontokon átmenő egyenesnek és a 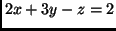 egyenletű síknak a
metszetét! (ZH. 2000. nov.)
egyenletű síknak a
metszetét! (ZH. 2000. nov.)
- Írd fel az
 ,
, 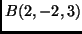 ,
,  pontokon
átmenő sík egyenletét!
pontokon
átmenő sík egyenletét!
- A
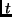 paraméter mely értékére lesz az alábbi három egyenlettel
megadott síkoknak egynél több közös pontja: (ZH. 1998. nov.)
paraméter mely értékére lesz az alábbi három egyenlettel
megadott síkoknak egynél több közös pontja: (ZH. 1998. nov.)
- Döntesd el, hogy az alábbiakban megadott
 alaphalmaz a
alaphalmaz a
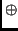 -szal jelölt vektorösszeadással és a
-szal jelölt vektorösszeadással és a 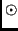 -tal jelölt
skalárral való szorzással vektorteret alkot-e?
-tal jelölt
skalárral való szorzással vektorteret alkot-e?
 az egész számok halmaza,
az egész számok halmaza, 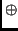 az egészek összeadása,
az egészek összeadása,
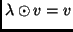 minden skalár és
minden skalár és 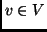 esetén.
esetén.
 a racionális számok halmaza,
a racionális számok halmaza, 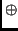 a racionális számok
összeadása,
a racionális számok
összeadása,
![$\lambda\odot v=\left[\lambda\cdot v\right]$](img26.png) , ahol
a
, ahol
a
![$\left[\quad\right]$](img27.png) a szám egészrészét jelöli.
a szám egészrészét jelöli.
 a pozitív valós számok halmaza,
a pozitív valós számok halmaza,
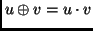 (azaz a
(azaz a
 a valós számok szorzása!),
a valós számok szorzása!),
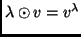 .
.
 a valós számok halmaza,
a valós számok halmaza,  , a skalárral való szorzás
a szokásos.
, a skalárral való szorzás
a szokásos.
- Fejezzük ki
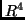 -ben az
-ben az 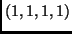 vektort az
vektort az 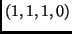 ,
, 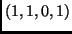 ,
,
 ,
, 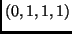 vektorok segítségével!
vektorok segítségével!
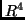 vektorai közül melyek fejezhető ki az alábbi vektorok segítségével:
vektorai közül melyek fejezhető ki az alábbi vektorok segítségével:
 ,
, 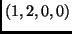 ,
, 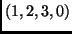 ,
, 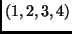 ?
?



Next: About this document ...
Veto Balint
2002-02-17
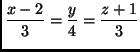 .
Írd fel az irányvektorát! Ennek segítségével határozd meg annak az egyenesnek
az egyenletrendszerét kétféleképpen (paraméteresen is), amely párhuzamos
.
Írd fel az irányvektorát! Ennek segítségével határozd meg annak az egyenesnek
az egyenletrendszerét kétféleképpen (paraméteresen is), amely párhuzamos
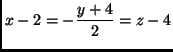 , és
, és
 egyenesek metszésponját!
egyenesek metszésponját!

 az egész számok halmaza,
az egész számok halmaza, 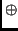 az egészek összeadása,
az egészek összeadása,
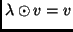 minden skalár és
minden skalár és 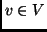 esetén.
esetén.
 a racionális számok halmaza,
a racionális számok halmaza, 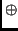 a racionális számok
összeadása,
a racionális számok
összeadása,
![$\lambda\odot v=\left[\lambda\cdot v\right]$](img26.png) , ahol
a
, ahol
a
![$\left[\quad\right]$](img27.png) a szám egészrészét jelöli.
a szám egészrészét jelöli.
 a pozitív valós számok halmaza,
a pozitív valós számok halmaza,
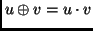 (azaz a
(azaz a
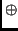 a valós számok szorzása!),
a valós számok szorzása!),
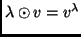 .
.
 a valós számok halmaza,
a valós számok halmaza,  , a skalárral való szorzás
a szokásos.
, a skalárral való szorzás
a szokásos.