Copyright © 2006 Zsolt Terék, terek@cs.bme.hu

Download PDF version

Formation of the Circumzenithal Arc

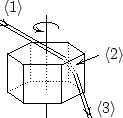
Circumzenithal arc is produced by the refraction of light on hexagonal ice crystals. If the crystals are plate shaped (their height is relatively small), their largest face is horizontally aligned due to different aerodinamic reasons. We will show how rays of Sun are refracted while passing through such oriented plate crystals.

Figure 1: The path of the light in a horizontally oriented plate crystal

Assuming parallel rays coming from the Sun, consider the rays that enter a hexagonal prism on its upper horizontal face and leave on one of the vertical sides. (See Figure 1.) The path of the light is made up by three segments: $\langle 1\rangle$ before entering, $\langle 2\rangle$ inside, $\langle 3\rangle$ after leaving the crystal.

The refraction at the boundary of segments $\langle 1\rangle$ and $\langle 2\rangle$ is invariant to any rotation of the prism around the vertical axis. Let $\alpha$ denote the elevation of the Sun, $\beta$ the angle between the horizontal plane and ligth segment $\langle 2\rangle$ and $n$ the refraction index of ice. According to Snell's law:

$$n = {\frac{\sin{(90^\circ-\alpha)}}{\sin{(90^\circ-\beta)}}} = {\frac{\cos\alpha}{\cos\beta}}$$ (1)

The refraction $\langle 2\rangle$/ $\langle 3\rangle$ at the vertical face $S$ of the prism is more interesting. Note that despite both pairs of segments $\langle 1\rangle$/ $\langle 2\rangle$ and $\langle 2\rangle$/ $\langle 3\rangle$ being coplanar, the two refraction planes are different in general. Instead of the current coordinate system having a fixed light ray segment $\langle 2\rangle$ and plane $S$ rotating freely around the vertical axis, we make $S$ fixed for the analysis below.

Figure 2: Coordinate system fixed to a vertical face of the prism

Figure 3: The plane of the second refraction

As depicted in Figure 2, let $X$ denote the intersection of ray $\langle 2\rangle$ and plane $S$, and $A$ a point of ray $\langle 2\rangle$ at some fixed height. In the coordinate system fixed to plane $S$, the possible locations for point $A$ form a circle. Let $O$ be the center of this circle, and $P_A$ the projection of $A$ onto the diameter of the circle that is in $S$. The refraction plane is defined by ray $\langle 2\rangle$ and the normal $\bf n$ of $S$ at $X$. Since $AP_A$ is parallel to $\bf n$, the plane of refraction contains $P_A$.

The next figure depicts the refraction $\langle 2\rangle$/ $\langle 3\rangle$. Let $A^\prime$ and $P_{A^\prime}$ be the images of $A$ and $P_A$ after a reflection in $X$, respectively. Let $B$ be a point on ray $\langle 3\rangle$ such that the lengths $\vert XA\vert$ and $\vert XB\vert$ are equal, furthermore $P_B$ be the projection of $B$ onto line $P_AP_{A^\prime}$. Finnally, let $C$ be the intersection of $XB$ and $A^\prime P_{A^\prime}$. Applying Snell's law gives:

$$n= {\sin\gamma^*\over\sin\beta^{*}} = {\vert XP_B\vert/\... ...rt\over\vert XC\vert} = {\vert XA\vert\over\vert XC\vert}$$ (2)

We are going to determine the possible locations of point $C$ while $A$ moves on the semicircular arc depicted above. Let $H$ denote the horizontal plane in which this circle lies, while $H^\prime$ is its reflection in $X$. Since $A^\prime \in H^\prime$, therefore $C\in H^\prime$. Beside, (2) states that $\vert XC\vert=\vert XA\vert/n$, which is constant, since all the points of the semicircle are equidistant from $X$. Thus $C$ is in the intersection of this sphere and plane $H^\prime$, which is a circle. Figure 4 shows plane $H^\prime$ including $O^\prime$, which is the reflection of $O$ in $X$.

Figure 4: The horizontal plane $H^\prime$

As a consequence of $C$ being on a circular arc in a horizontal plane, the angle of ray $\langle 3\rangle$ to the vertical line is independent of the orientation of the crystal. The circumzenithal arc is therefore produced by the ice crystals that are on the cone, which has a vertical axis and its apex is at the viewer.

Below we express the angle $\gamma$ under which the arc is seen and the angular width $\varphi$ of the arc in therms of the elevation of the sun ($\alpha$). Consider the vertical plane in which rays $\langle 1\rangle$ and $\langle 2\rangle$ lie. If the side face $S$ of the hexagonal crystal is perpendicular to this plane, ray $\langle 3\rangle$ also lies in this plane. This implies $AO \perp S$ and $P_A=O$, therefore $\beta^*=\beta$ and $\gamma^*=\gamma$. From (1) and (2) recall that

$$n={\cos\alpha\over\cos\beta},\quad n={\sin\gamma\over\sin\beta}.$$ (3)

Based on these,

$$\sin^2\gamma = n^2\sin^2\beta = n^2\left(1-{\cos^2\alpha\over n^2}\right) = n^2 - \cos^2\alpha.$$ (4)

Since $n\approx 1.309>1$, this is always positive. A necessary condition for the appearance of the circumzenithal arc follows from the fact that $\sin\gamma \le 1$, thus

$$n^2 - \cos^2\alpha \le 1,$$ (5)

$$\alpha \le \cos^{-1} \sqrt{n^2-1} \approx 32.36^\circ.$$ (6)

Therefore if $\alpha\in[0,32.36]$, the angular radius of the arc is

$$\gamma = \sin^{-1} \sqrt{n^2 - \cos^2\alpha}.$$ (7)

The angular width $\varphi$ of the arc can be calculated as follows. The path of the light projected into the horizontal plane $H^\prime$ is shown in Figure 4 using double stripped lines. The maximum deviation of the light in the horizontal plane is the half of the angular width circumzenithal arc. The maximum deviation angle corresponds to the angle of total reflection, i.e., when $P_{A^\prime}=C$, thus

$$\varphi/2 = \angle CO^\prime P_{A^\prime},$$ (8)

so the ratio of the circles' radii in $H^\prime$ is

$$\cos{\varphi\over 2} = {\vert O^\prime P_{A^\prime}\vert\over \vert O^\prime A^\prime\vert} = r/R.$$ (9)

To obtain the ratio of the radii, consider again the case when all 3 ray segments are in the same vertical plane. Using the notations of Figure 3, having $\beta=\beta^*$ and $\gamma=\gamma^*$ and using (2) this can be written as

$${r/R} = {\vert P_{A^\prime}A^\prime\vert\over \vert P_{... ...rt\cos\beta} = {1\over n}\cdot{\cos\gamma\over\cos\beta}.$$ (10)

With the help of equations 3,

$$\cos^2{\varphi\over 2}={1\over n^2}\cdot {\cos^2\gamma\ove... ...2\alpha)\over\cos\alpha} = 1+{1-n^2\over\cos^2\alpha}.$$ (11)

Condition for this being positive leads to the same constraints that we got for (4). Obviously, this is less than $1$, therefore for the prevoiusly defined range of $\alpha$, the angular with of the circumzenithal arc is

$$\varphi = 2\cos^{-1} \sqrt{1+{1-n^2\over\cos^2\alpha}}.$$ (12)