1. ábra
| BME Villamosmérnöki és Informatikai Kar
Mérnök-informatikus mesterszak |
Nappali tagozat
2023/2024-es tanév, tavaszi félév
|
A megoldandó feladat a közismert Sudoku egy variánsa (n-away sudoku).
Sudoku-mátrixnak hívunk egy olyan négyzetes mátrixot, amelyben a sorok (és az oszlopok) száma egy m = k2 ≥ 1 négyzetszám. (Tehát a mátrix elemeinek száma m2 = k4.)
Egy Sudoku-mátrixban cellának hívunk egy olyan (folytonos) részmátrixot, amely k sorból és k oszlopból áll, és bal felső sarkának sor- ill. oszlopindexe i*k+1 ill. j*k+1, ahol 0 ≤ i,j ≤ k-1 (a sorokat és oszlopokat 1-től indexeljük).
A Sudoku-mátrix elemeit mezőknek is nevezzük.
Egy Sudoku-feladvány két részből áll. Az egyik rész egy olyan Sudoku-mátrix, amelynek egyes mezői segítő információkat (röviden infókat) tartalmaznak, ezt infómátrixnak nevezzük. A Sudoku játék közismert alapváltozatában csak ún. száminfók fordulnak elő, amelyek azt írják elő, hogy a megoldás adott mezője egy adott számot tartalmazzon.
A feladvány másik része egy n távolságkonstans, amely az ún. távolságinfók értelmezéséhez szükséges, ahol 1 ≤ n ≤ m-1.
Nevezzünk értékmátrixnak egy olyan Sudoku-mátrixot, amelynek mezői egész számok. Egy m*m méretű Sudoku-feladvány megoldása egy m*m méretű értékmátrix, ha
A jelen házi feladatban a száminfók mellett egy további fajta segítő
információ fordulhat elő: a távolságinfó.
A távolságinfó azt az információt hordozza, hogy az adott
mezőben valamint egy megadott szomszédos mezőben levő
értékek távolsága n.
Két érték távolságán különbségük abszolút értékét értjük.
A távolságinfó kétféle lehet: déli és nyugati, ezek
jelölése rendre s és w.
A déli távolságinfó azt írja elő, hogy az adott mező
értéke n távolságra van az alatta
levő mező értékétől, míg a nyugati ugyanezt állítja az adott mező baloldali szomszédjáról.
A feladvány az összes lehetséges távolságinfót tartalmazza. Tehát ha a
Sudoku-feladvány egy mezője nem tartalmazza az s
(w) infót, akkor biztos, hogy az adott mező és a déli
(nyugati) szomszédja közötti távolság nem n. Másszóval egy
értékmátrix nem megoldás, ha egy olyan oldalszomszédos mezőpárt
tartalmaz, amelyek távolsága n, és ugyanakkor a pár északi
(keleti) mezője a feladványban nem tartalmazza az s
(w) távolságinfót.
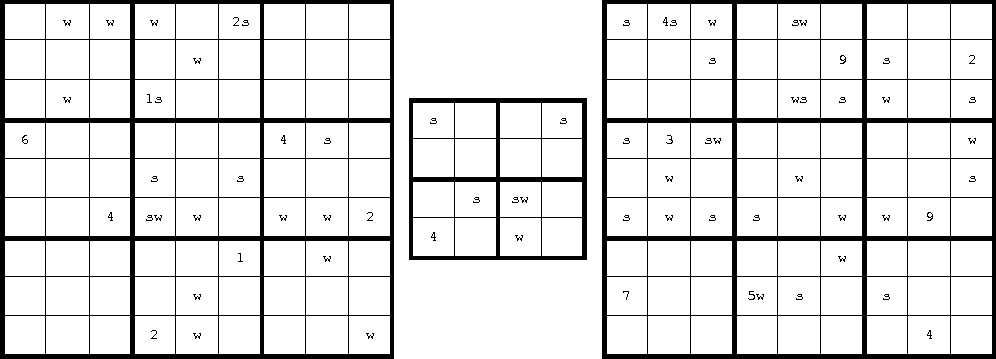
Három Sudoku-feladványt mutatunk az 1. ábrán, ahol a k cellaméret és az n távolságkonstans rendre k=3, n=2; k=2, n=1 és k=3, n=3.

A legegyszerűbb esetben az infó egy szám: az adott mező előírt értéke. A további infókat egybetűs azonosítókkal jelezzük. A száminfótól különböző előírásokból többféle is lehet egy mezőben. A feladványokban betűk jelzik a távolságinfókat, ezek jelentése:
s (south): az adott és az alatta levő mező értékének
távolsága n, w (west): az adott és a tőle balra levő mező értékének
távolsága n.
A Sudoku-feladvány bal szélső oszlopának mezőiben nem állhat w, alsó
sorának mezőiben pedig s, mivel ezek az infók nem létező
mezőkre vonatkoznának.
Egy mezőben a háromféle infó (a száminfó ill. a kétféle, betűkkel jelzett infók) mindegyike legfeljebb egyszer szerepelhet.
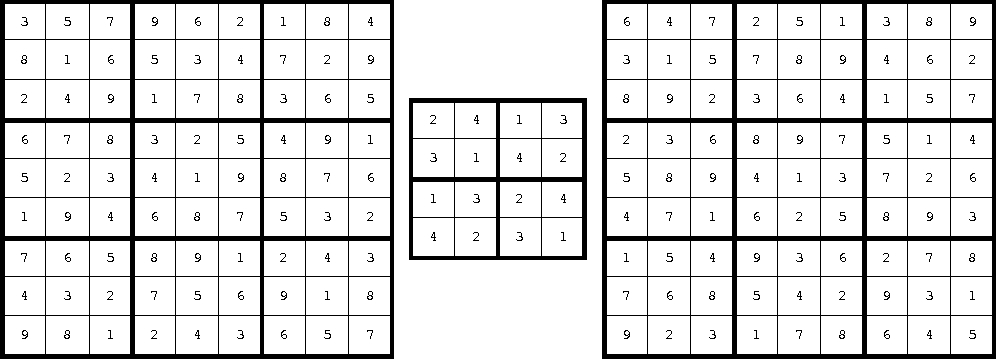
Az 1. ábrán látható három feladvány egy-egy megoldását a 2. ábra mutatja. Mindhárom feladványnak ez az egyetlen megoldása.
Írjon sudoku néven egy olyan, a clpfd könyvtárat
felhasználó Prolog-eljárást, amely egy feladvány összes megoldását
előállítja!
A Prolog-eljárásnak két paramétere van. Első (bemenő) paramétere a feladványt, második (kimenő) paramétere a megoldást írja le. Az eljárásnak a visszalépések során minden megoldást pontosan egyszer kell kiadnia (tetszőleges sorrendben). Ez azt is jelenti, hogy ha a feladványnak nincs megoldása, az eljárásnak meg kell hiúsulnia.
A Prolog-eljárás bemenő paramétere egy
s(N,T)
felépítésű struktúra, ahol
N a távolságkonstans,T a sorok listájaként megadott feladvány, ahol egy sor a benne
levő mezők listája.
A feladvány egy mezőjét infók listájaként adjuk meg. Infó lehet
az
s és w atom, továbbá az 1 ≤ I ≤
m szám lehet. Az
infók listájában mindegyik atom illetve szám legfeljebb egyszer,
de tetszőleges sorrendben fordulhat elő, és a lista üres is lehet.
A Prolog-eljárás kimenő paramétere a feladvány egy megoldása, amelyet számokat tartalmazó listák listájaként ábrázolunk.
Például az 1. ábra középső feladványát a következő Prolog-struktúrával írjuk le:
s(1, [[ [s], [], [], [s]],
[ [], [], [], []],
[ [], [s], [s,w], []],
[ [4], [], [w], []]])
A feladvány egyetlen megoldását a következő lista írja le:
[[ 2, 4, 1, 3],
[ 3, 1, 4, 2],
[ 1, 3, 2, 4],
[ 4, 2, 3, 1]]
| ?- sudoku(s(1, [[[s], [], [],[s]],
[ [], [], [], []],
[ [],[s], [s,w], []],
[ [], [], [w], []]
]
), Sol).
Sol = [[3,1,4,2],
[2,4,1,3],
[4,2,3,1],
[1,3,2,4]] ? ;
Sol = [[2,4,1,3],
[3,1,4,2],
[1,3,2,4],
[4,2,3,1]] ? ;
no
| ?- sudoku(s(1, [[[s], [], [],[s]],
[ [], [], [], []],
[ [],[s], [s,w], []],
[[4], [], [], []]
]
), Sol).
no
A sudoku/2 Prolog-eljárás típusát a következő -
megjegyzésként megadott - Prolog-típusdefiníciók írják le.
% :- type sspec ---> s(dist, board).
% :- type dist == int.
% :- type field == list(info).
% :- type info ---> s; w; int.
% :- type board == list(list(field)).
% :- type ssol == list(list(int)).
% sudoku(SSpec, SSol):
% SSol az SSpec feladványt kielégítő megoldás.
% :- pred sudoku(sspec::in, ssol::out).
Programját keretprogram segítségével próbálhatja ki. A keretprogramot a beadáskor használthoz hasonló tesztesetekkel együtt innen töltheti le. A nagy házi feladatok teszteléséhez és értékeléséhez a keretprogrammal azonos specifikációjú programot fogunk használni.
A keretprogram bemenete egy olyan szövegfájl, amelynek első nem üres sora a
Sudoku-feladvány távolságkonstansát, minden egyes további nem üres sora a
Sudoku-feladvány egy-egy sorát tartalmazza, ahol az egyes mezők értékét egy
vagy több szóköz választja el. A - karakter jelzi, ha egy
mező nem tartalmaz infót. Ha tartalmaz, a mezőt az infók felsorolásával
adjuk meg: a számot decimális alakban, a többi infót a betűjelével írjuk
le; a jelek közé nem szabad szóközt tenni.
Például az 1. ábra közepső Sudoku-feladványát a 3. ábrán látható módon ábrázoljuk a bemeneti szövegfájlban:
1 s - - s - - - - - s sw - 4 - w -3. ábra
A keretprogram kimenete a 4. ábrán bemutatotthoz hasonló tartalmú szövegfájl.
----- 2 4 1 3 3 1 4 2 1 3 2 4 4 2 3 1 -----4. ábra
A ksudoku.pl Prolog-keretprogram a következő eljárásokat
exportálja:
% :- pred sudoku_be(file::in, sspec::out).% :- pred sudoku_ki(file::in, ssol::in).% :- pred megold(file::in, file::in).sudoku/2 eljárást.% :- pred stopper(file::in, file::in).megold/2, de a végén kiírja a feladvány nevét, a
megoldások számát és a futási időt is.
% :- pred teljes_teszt(int::in).
tests könyvtárban levő összes testXXXd.txt
tesztállomány esetén:
testXXXs.txt állományban megadott
megoldáshalmazt kapta,
megold/2) kiírja az eredményt a tests_out
könyvtár testXXXt.txt nevű állományába.
XXX egy tetszőleges hosszúságú
számjegysorozatot jelöl.
Ezt az eljárást Eisenberger András ültette át Prologra.
A keretprogram felhasználja a file típust:
% :- type file == atom.
A file típusú paraméterben a user atomot megadva
a terminálról vihetünk be, ill. a terminálra írathatunk ki adatokat.
Egyébként a megadott nevű fájlba írunk, ill. fájlból olvasunk.
Használat: saját programját a
sudoku.pl nevű fájlba tegye, különben a
ksudoku.pl keretprogram nem találja meg. Ezután indítsa el a
SICStus rendszert, és töltse be a keretprogramot. Példa:
SICStus 4.6.0 (...)
Licensed to BUTE DP Course
| ?- [ksudoku].
% compiling /home/szeredi/tmp/ksudoku.pl...
% module sudoku_keret imported into user
(...)
% compiled /home/szeredi/tmp/ksudoku.pl in module sudoku_keret, 30 msec 78104 bytes
yes
| ?- stopper('teszt0.txt','teszt0.sol').
A stopper/2, ill. megold/2 eljárások meghívása a
sudoku.pl programot automatikusan betölti (ha szükséges),
ezért ennek módosításakor nem kell sem a SICStus interpretert
újraindítania, sem a keretprogramot újra betöltenie.
A programot úgy írja meg (választása szerint vagy magyarul, vagy angolul), hogy a szövege jól olvasható legyen: válasszon értelmes neveket, specifikálja a paraméterek és más azonosítók szerepét és értelmezési tartományát, magyarázza meg az egyes eljárások, ill. függvények feladatát és működését! Kövesse a Prolog diákon használt szövegelrendezési konvenciókat! Ne írjon hosszú sorokat! Minden eljáráshoz és függvényhez készítsen fejkommentet!
A programhoz készítsen dokumentációt; vagy magyarul, vagy angolul. A dokumentáció tartalma legalább a következő legyen:
Fogalmazzon világosan és tömören, ügyeljen a helyes nyelvhasználatra és a helyesírási szabályok betartására! Az indokoltan elvárható formai követelmények be nem tartását, a gondatlan kivitelt szankcionáljuk.
A dokumentációt elektronikus alakban adja be PDF formátumban.
A program készülhet MS Windows alatt is, de Linux alatt is működnie kell. A beadott programokat Linux környezetben a SICStus Prolog 4 rendszerrel teszteljük.
A programot és az elektronikus dokumentációt webes felületen lehet külön-külön feltölteni az Elektronikus Tanársegéd HF beadás menüpontjában. A beadást többször is megismételheti, az utoljára beadott megoldást tekintjük érvényesnek.