


Next: About this document ...
Sziasztok!
1. Volt először is villámzh az ora elején, eredmények itt.
2. Zh kiosztás, pótzh-val kapcsolatos hirdetnivalók:
időpontja: 2000. április 25., a húsvét utáni kedd, 16.00-tól 18.00-ig.
A termeket és a beosztást később megírom, illetve a jövő héten kihirdetjük
az órán is. Pótzh-t bárki írhat és senkinek sem kötelező írnia.
Az első 20 perc után ott lehet hagyni a pótzh-t és ki lehet jönni, akkor
olyan, mintha nem is írtál volna. Ha viszont maradsz, akkor a félévi
pontszámba a pótzh és a rendes zh átlaga számít.
3. A mai óra anyaga általános elemzők: ezek olyan elemzők, amik minden CF
nyelvre mennek, nem kell, hogy a nyelv egyértelmű legyen, meg az se
kell, hogy a nyelvtan, amiben elemzünk ne legyen balrekurzív.
Két ilyen algoritmust tanulunk:
a Cocke-Younger-Kasami (CYK) és az Earley algoritust.
Megcsináltuk az órán az 1. és a 2. feladatot, a többi elemzős feladat
gyakorolni van. Ha csináltok velük valamit, szívesen kijavítom.
Segítségül:
nagyon röviden a CYK algoritmusról
kicsit hosszabban az Earley algoritmusról.
A jegyzetben is van kidolgozott példa mindkettőre, ott is lehet tájékozódni.
Általános elemzők
Formális nyelvek gyakorlat (9)
2000. április 11., kedd
1. A Coke-Younger-Kasami módszer segítségével határozzuk meg
az aabbbc szó összes jobboldali levezetését, ha a nyelvtan
a következő:
2. Legyen a nyelvtanunk a következő:
 ,
,
 ,
,
 . Elemezzük az Earley algoritmussal a bdvuvuve szót!
. Elemezzük az Earley algoritmussal a bdvuvuve szót!
3. Még mindig az Earley algoritmus: a nyelvtan az
 .
Az elemzendő szó: aababbab.
.
Az elemzendő szó: aababbab.
Gyakorolni
4.
A CYK elemzéssel elemezzük az
 nyelvtanban az abbbba és az
abbba szót!
nyelvtanban az abbbba és az
abbba szót!
5. A CYK algoritmussal (elemzéssel) elemezzük az
 nyelvtanban az
nyelvtanban az
(a) a+a*a+a szót
(b) a++a szót!
Döntsük el, hogy generálhatók-e a nyelvtannal, egyértelműen generálhatók-e és
adjuk meg a levezetési fákat is!
6. Earley algoritmussal elemezzük az a+a*a szót az
 nyelvtanban. Gondoljuk végig, hogy hol látszik az elemzésben az, hogy nem
egyértelmű a nyelvtan!
nyelvtanban. Gondoljuk végig, hogy hol látszik az elemzésben az, hogy nem
egyértelmű a nyelvtan!
Hogy ne unatkozzatok, ha már az összess eddigivel megvagytok:
7. Növekedne-e a veremautomata ereje,
ha két vermet engednénk meg?
Azaz, mi lenne, ha a veremautomata szabályai
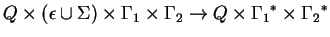 alakúak volnának?
(A békesség kedvéért legyen állapottal elfogadó az automata.)
alakúak volnának?
(A békesség kedvéért legyen állapottal elfogadó az automata.)
8.
Az ismert
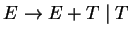 ,
,
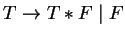 ,
,
 nyelvtan generál
felesleges zárójeleket, például az (a*a)+a vagy az (a) generálásakor.
Alakítsuk át úgy a nyelvtant, hogy ne tegye ezt!
nyelvtan generál
felesleges zárójeleket, például az (a*a)+a vagy az (a) generálásakor.
Alakítsuk át úgy a nyelvtant, hogy ne tegye ezt!



Next: About this document ...
Judit Csima
2000-04-13

