Bevezetés a számításelméletbe II.
2002. április 18.
1. ZH! Bizonyítsuk be, hogy
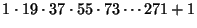 osztható 17-tel!
osztható 17-tel!
2. ZH! Legyen a valós számok halmazán értelmezve a következő művelet:
 . Vizsgáljuk meg, hogy ez a művelet asszociatív-e,
kommutatív-e, van-e egységeleme és hogy invertálható-e.
. Vizsgáljuk meg, hogy ez a művelet asszociatív-e,
kommutatív-e, van-e egységeleme és hogy invertálható-e.
3. Félcsoportot, illetve
csoportot alkotnak-e az adott halmazok az adott muveletekre nézve?
Ha csoport, akkor kommutatív-e? Ha csoport, akkor adj meg egy részcsoportot
is benne.
(a) (páros számok, +),
(b) (páros számok,  ),
),
(c) (pozitív számok, +)
4. ZH! Legyen a  csoport elemeinek halmaza
csoport elemeinek halmaza
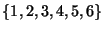 , a művelet
pedig a szorzás
, a művelet
pedig a szorzás  . Igazoljuk, hogy
. Igazoljuk, hogy  ciklikus.
ciklikus.
5. ZH! Legyen  kommutatív csoport és
kommutatív csoport és 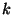 rögzített pozitív
egész szám.
rögzített pozitív
egész szám. 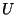 jelölje
jelölje  azon elemeinek
halmazát, amelyek eloállnak valamely
azon elemeinek
halmazát, amelyek eloállnak valamely  -beli elem
-beli elem 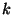 -adik
hatványaként, vagyis
Mutassuk
meg, hogy
-adik
hatványaként, vagyis
Mutassuk
meg, hogy 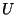 részcsoport
részcsoport  -ben!
-ben!
6. (a) Mik az egyes elemek rendjei a  rendu ciklikus csoportban?
rendu ciklikus csoportban?
(b) ZH! Hány olyan eleme van a 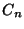 ciklikus csoportnak, ami egymaga
generálja a teljes
ciklikus csoportnak, ami egymaga
generálja a teljes 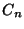 csoportot?
csoportot?
7. HF, ZH! Állapítsuk meg, hogy izomorf-e a mod 4 maradékosztályok additív
csoportja a mod 8 maradékosztályok multiplikatív csoportjával!
8. Mi lesz
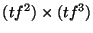 a szabályos ötszög
egybevágóságait leíró csoportban (azaz
a szabályos ötszög
egybevágóságait leíró csoportban (azaz
 -ben, az ötödfokú diédercsoportban)?
-ben, az ötödfokú diédercsoportban)?
9. ZH! Mutassuk meg, hogy az olyan kétszer kettes valós 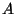 mátrixok,
amelyekben a két foátlóbeli elem
mátrixok,
amelyekben a két foátlóbeli elem 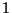 -gyel egyenlo, a bal alsó
sarokban pedig 0 áll (tehát
-gyel egyenlo, a bal alsó
sarokban pedig 0 áll (tehát
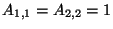 ,
, 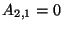 és
és
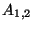 tetszoleges valós szám) csoportot alkotnak a
mátrixszorzás muveletére nézve!
tetszoleges valós szám) csoportot alkotnak a
mátrixszorzás muveletére nézve!
10. ZH! Igazoljuk, hogy egy csoport nem állhat elő két valódi
részcsoportjának uniójaként.
11. Legyen 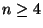 . Az
. Az 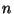 hosszú
hosszú 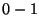 sorozatok halmazán jelölje
sorozatok halmazán jelölje 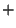 a
a
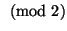 összeadást, azaz
összeadást, azaz
 , ha
, ha
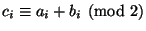 teljesül minden
teljesül minden
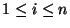 esetén.
Álljon
esetén.
Álljon 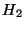 azon
azon 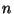 hosszú
hosszú 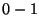 sorozatokból, melyekben az egyesek száma
osztható kettővel,
sorozatokból, melyekben az egyesek száma
osztható kettővel,  pedig azon
pedig azon 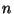 hosszú
hosszú 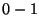 sorozatokból, melyekben az egyesek száma
osztható hárommal. Az előbb definiált művelettel csoport-e
sorozatokból, melyekben az egyesek száma
osztható hárommal. Az előbb definiált művelettel csoport-e 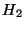 ? És
? És  ?
?
12. ZH! Bizonyítsuk be, hogy
 osztható 1999-cel!
osztható 1999-cel!
13. Zárt-e az irracionális számok halmaza az összeadásra? Zárt-e a pozitív racionális számok halmaza az osztás műveletre? Van-e a pozitív racionális számok körében minden számnak inverze a szorzásra nézve? Van-e a nemnegatív egészek körében minden számnak inverze az összeadásra nézve?
14. A
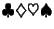 halmazon az ábrán megadott két műveletet értelmezzük (pl.
halmazon az ábrán megadott két műveletet értelmezzük (pl.
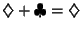 ).
).
- Mennyi

- Kommutatív illetve asszociatív-e ez a két művelet? Van-e egységelem?
- Oldjuk meg a
 egyenletet!
egyenletet!
15. Csoportot alkotnak-e az alábbiak:
-
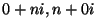 , (
, (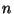 egész) alakú komplex számok az összeadás művelettel
egész) alakú komplex számok az összeadás művelettel
-
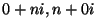 , (
, (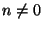 egész) alakú komplex számok a szorzás művelettel
egész) alakú komplex számok a szorzás művelettel
-
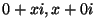 , (
, (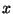 valós) alakú komplex számok az összeadás művelettel
valós) alakú komplex számok az összeadás művelettel
-
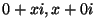 , (
, (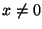 valós) alakú komplex számok a szorzás művelettel
valós) alakú komplex számok a szorzás művelettel
- a valós számok a hatványozással
16. ZH! Álljon 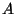 azokból a
azokból a  mátrixokból, melyeknek mind a négy
eleme ugyanaz a pozitív valós szám. Csoportot alkot-e ez a halmaz a szokásos
mátrixszorzással?
mátrixokból, melyeknek mind a négy
eleme ugyanaz a pozitív valós szám. Csoportot alkot-e ez a halmaz a szokásos
mátrixszorzással?
17. ZH! Az 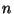 -ed rendű ciklikus csoport összes elemét négyzetre emeljük,
majd az így kapott elemeket össszeszorozzuk. Mivel egyenlő ez a szorzat?
-ed rendű ciklikus csoport összes elemét négyzetre emeljük,
majd az így kapott elemeket össszeszorozzuk. Mivel egyenlő ez a szorzat?
18. ZH! Tekintsük az
 alakú lineáris függvényeket,
ahol
alakú lineáris függvényeket,
ahol 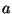 nem nulla valós,
nem nulla valós,  tetszoleges valós szám.
Legyen a
tetszoleges valós szám.
Legyen a 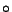 muvelet a függvények összetétele, azaz
muvelet a függvények összetétele, azaz
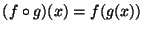 .
Igazoljuk, hogy erre a muveletre nézve az adott függvények
csoportot alkotnak! Mi a csoport egységeleme?
.
Igazoljuk, hogy erre a muveletre nézve az adott függvények
csoportot alkotnak! Mi a csoport egységeleme?
19. * Igaz-e, hogy minden csoportban
(a)
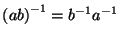
(b)
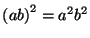
(c) Igaz-e ez kommutatív csoportban?
(d) Bizonyítsuk be, hogy
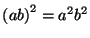 pontosan akkor teljesül
minden
pontosan akkor teljesül
minden 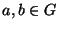 -re, ha
-re, ha  kommutatív.
kommutatív.
(e) Igaz-e ugyanez
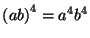 -nel?
-nel?
20. * Legyen  csoport a
csoport a  művelettel és legyen
művelettel és legyen 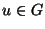 egy
kiválasztott elem
egy
kiválasztott elem  -ben. Csoport-e
-ben. Csoport-e  az
az
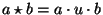 művelettel?
művelettel?
21. * Bizonyítsuk be, hogy tetszoleges prímre
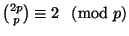 .
.
Csima Judit
2002-04-18
