Bevezetés a számításelméletbe II.
2002. április 11.
1. Ha
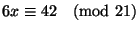 , akkor az alábbiak közül mi igaz biztosan?
, akkor az alábbiak közül mi igaz biztosan?
(a)
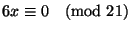
(b)
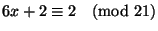
(c)
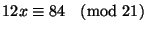
(d)
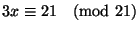
(e)
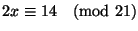
(f)
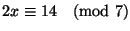
2. Milyen maradékot adhat 45-tel osztva az 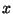 szám, ha
szám, ha
 ?
?
3. ZH! Bizonyítsuk be, hogy 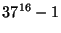 osztható
osztható  -tel.
-tel.
4. HF, ZH! Legyenek 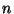 és
és 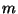 olyan pozitív egészek, melyekre
olyan pozitív egészek, melyekre 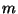 osztója
osztója 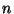 -nek.
Bizonyítsuk be, hogy
-nek.
Bizonyítsuk be, hogy 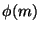 osztója
osztója 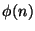 -nek.
-nek.
5. Tudjuk, hogy az 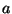 egész számra teljesül, hogy
egész számra teljesül, hogy
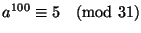 és
és
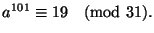 Milyen maradékot ad 31-gyel való osztáskor az
Milyen maradékot ad 31-gyel való osztáskor az 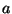 egész szám?
egész szám?
6. (a) Melyik a nagyobb,  vagy
vagy
 ?
?
(b) ZH! Határozzuk meg a 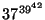 utolsó két számjegyét.
utolsó két számjegyét.
7. Mely 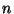 -ekre lesz
-ekre lesz 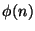 prímszám?
prímszám?
8. ZH! Oldjuk meg az 
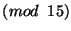 kongruenciát.
kongruenciát.
9. Határozzuk meg az összes olyan természetes 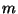 számot és
számot és 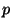 prímszámot,
melyre
prímszámot,
melyre
 .
.
10. ZH! Határozzuk meg  utolsó két számjegyét!
utolsó két számjegyét!
11. ZH! Milyen maradékot adhat 45-tel osztva az 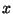 szám, ha
szám, ha 

12. ZH! Bizonyítsuk be, hogy
 .
.
13. ZH! Legyen 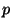 és
és 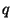 két prímszám és
két prímszám és 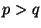 . Adjuk meg az összes olyan
. Adjuk meg az összes olyan 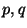 számpárt, melyre
számpárt, melyre 
 .
.
14. ZH! Relatív prím-e a 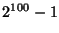 és
és 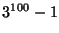 ?
?
15. Keressük meg 7 azon pozitív többszöröseit, melyek
13-mal osztva 11-et adnak maradékul!
16. Bizonyítsuk be, hogy ha  osztója
osztója 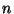 -nek, akkor
-nek, akkor
 .
.
17. ZH! Legyen 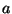 egy 2001-hez relatív prím szám. Bizonyítsuk be, hogy ekkor
egy 2001-hez relatív prím szám. Bizonyítsuk be, hogy ekkor
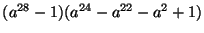 osztható 2001-gyel. (
osztható 2001-gyel. (
 )
)
18. Milyen maradékot adhat 72-vel osztva az 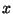 szám, ha
szám, ha 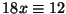
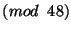
19. * Mely 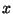 -ekre teljesül mindhárom alábbi kongruencia?
-ekre teljesül mindhárom alábbi kongruencia?
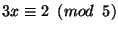

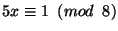
20. * Bizonyítsuk be, hogy 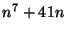 osztható
osztható  -vel, ha
-vel, ha 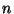 tetszoleges egész szám.
tetszoleges egész szám.
Csima Judit
2002-04-11