Bevezetés a számításelméletbe II.
2002. április 4.
1. (a) Határozzuk meg az 504 és a 372 prímtényezős felbontását!
(b) Mennyi  ? És
? És
 ?
?
(c) Az Euklideszi algoritmussal is határozzuk meg  -t!
-t!
(d) Írjuk fel  -t
-t 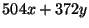 alakban!
alakban!
(e) Mennyi 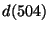 és
és  ?
?
2. Legyen  és
és  páratlan. Mennyi
páratlan. Mennyi
 ?
?
3. Van-e olyan pozitív egész 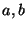 pár, hogy
pár, hogy 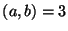 és
és  ?
És olyan, hogy
?
És olyan, hogy 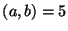 és
és  ?
Ahol igen, ott hányféle?
?
Ahol igen, ott hányféle?
4. ZH! Egy XX. században született emberről azt tudjuk, hogy épp nagyapja 59.
születésnapján született és hogy kettejük születési évszámai nem
relatív prímek. Mikor született az ember?
5. ZH! Melyik az a legkisebb pozitív háromjegyű szám, amelyiknek ötször annyi
páros osztója van, mint páratlan?
6. HF, ZH! Legyen  pozitív egész szám, melynek ismerjük
pozitív egész szám, melynek ismerjük
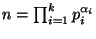 prímtényezos felbontását.
prímtényezos felbontását.
Mennyi a
érték, vagyis hogyan
számítható ki az  szám osztói reciprokának az összege?
szám osztói reciprokának az összege?
7. ZH! Legyen 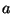 páratlan,
páratlan, 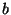 pedig páros szám. Igazoljuk, hogy ha
pedig páros szám. Igazoljuk, hogy ha
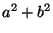 négyzetszám, akkor
négyzetszám, akkor 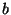 osztható néggyel.
osztható néggyel.
8. HF Bizonyítsuk be, hogy
 végtelen sok
végtelen sok  -re teljesül.
-re teljesül.
9. HF, ZH! Legyen 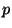 7-hatvány,
7-hatvány,  pedig 5-hatvány. Bizonyítsuk be, hogy léteznek
olyan
pedig 5-hatvány. Bizonyítsuk be, hogy léteznek
olyan 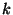 és
és 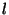 pozitív egészek, hogy ha egy
pozitív egészek, hogy ha egy 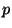 -fejű sárkány minden fejének
-fejű sárkány minden fejének
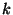 darab és egy
darab és egy  fejű sárkány minden fejének
fejű sárkány minden fejének 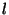 darab almát adunk, akkor
valamelyik sárkánynak épp egy almával jut több!
darab almát adunk, akkor
valamelyik sárkánynak épp egy almával jut több!
10. Határozzuk meg az Euklideszi algoritmussal  -t, majd írjuk fel
-t, majd írjuk fel
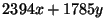 alakban.
alakban.
11. ZH! Egy 2000-ben születo embernek 90 éves koráig hány olyan
születésnapja lesz, amikor az életkora osztója az aktuális
évszámnak?
12. Maximum hány szám választható ki 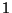 -tol
-tol 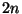 -ig úgy, hogy közülük semelyik ketto se
legyen relatív prím?
-ig úgy, hogy közülük semelyik ketto se
legyen relatív prím?
13. Melyek azok a 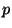 prímszámok, amelyekre
prímszámok, amelyekre  és
és 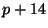 is
prímszám?
is
prímszám?
14. ZH! Hány olyan (pozitív) osztója van 3960-nak, amely 30
többszöröse?
15. ZH! Határozzuk meg az összes olyan 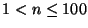 egész számot,
amelyekre teljesül, hogy
egész számot,
amelyekre teljesül, hogy  osztóinak száma háromhatvány.
osztóinak száma háromhatvány.
16. *
Egy perzsa sahnak száz felesége és száz rabja van,
utóbbiak külön cellákban sínylődnek. A sah születésnapján a kedvenc feleség
minden zárka zárján fordít egyet, a második kedvenc feleség minden
másodikon kettőt, az 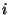 -edik minden
-edik minden 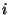 -ediken
-ediken 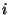 -t.
A zárak egy fordításra nyílnak, újabbra bezárulnak. Kérdés, hogy mely
cellák lesznek nyitva a nap végén.
-t.
A zárak egy fordításra nyílnak, újabbra bezárulnak. Kérdés, hogy mely
cellák lesznek nyitva a nap végén.
17. ZH, *
Legyenek 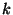 és
és  olyan pozitív egészek, amelyekre
olyan pozitív egészek, amelyekre 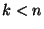 .
Mi a legnagyobb közös osztója az
.
Mi a legnagyobb közös osztója az 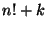 és az
és az 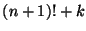 számoknak?
számoknak?
18. *Bizonyítsuk be, hogy minden 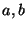 pozitív egészre
pozitív egészre
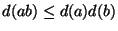 és egyenloség pontosan akkor teljesül, ha
és egyenloség pontosan akkor teljesül, ha 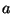 és
és
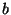 relatív prímek!
relatív prímek!
Csima Judit
2002-04-04