Bevezetés a számításelméletbe II.
2002. március 28.
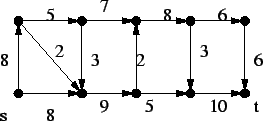
1. Adjunk meg egy maximális folyamot az alábbi hálózatban:
2. Határozzuk meg, hogy melyik az a legnagyobb 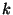 érték, amire
érték, amire
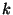 -szorosan pont-, illetve élösszefüggők az alábbi gráfok:
-szorosan pont-, illetve élösszefüggők az alábbi gráfok:
(a) 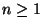 hosszú út (b)
hosszú út (b)  hosszú kör (c)
hosszú kör (c) 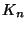 (
(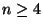 )
)
3. (a) Igaz-e, hogy ha minden él kapacitása páros szám, akkor van
olyan maximális folyam, aminek minden élén a folyam értéke
páros szám?
(b) Igaz-e ugyanez páratlan számokkal?
4. ZH! Melyik az a legnagyobb 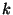 szám, amelyre
szám, amelyre 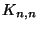 teljes páros gráf
teljes páros gráf
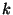 -szorosan pontösszefüggő?
-szorosan pontösszefüggő?
5. HF, ZH! Bizonyítsuk be, hogy ha egy 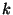 -szorosan pontösszefüggő
-szorosan pontösszefüggő
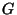 gráfból elhagyunk egy élet, akkor a kapott gráf
gráfból elhagyunk egy élet, akkor a kapott gráf 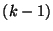 -szeresen
pontösszefüggő lesz.
-szeresen
pontösszefüggő lesz.
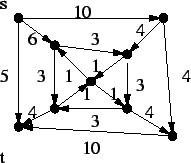
6. ( 16 jön ki ) Adjunk meg az alábbi ábrán látható hálózatban egy maximális folyamot!
7. HF Bizonyítsuk be, hogy ha egy gráf 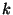 -szorosan pontösszefüggő akkor
-szorosan pontösszefüggő akkor
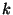 -szorosan élösszefüggő is.
-szorosan élösszefüggő is.
8. ZH! Egy hálózat gráfja a kocka élhálózata az ábrán látható irányítással.
(A forrás és a nyelő a kocka két átellenes pontja, lásd az ábrán.)
Az éleket vagy 1 vagy 2 kapacitásúnak választhatjuk meg a következő
feltételek mellett:
(a) az elérhető maximális folyam értéke a lehető legnagyobb legyen,
(b) az (a) feltétel teljesülése mellett minél kevesebb 2 kapacitású él
legyen.
Hány 2 kapacitású élre van szükség és melyek lesznek ezek?
9. ZH! A 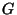 összefüggő, legalább 3 pontot tartalmazó
gráfban minden
összefüggő, legalább 3 pontot tartalmazó
gráfban minden 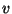 pontra és
pontra és  élre teljesül az, hogy van
élre teljesül az, hogy van
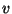 -n és
-n és  -n is átmenő kör. Mutassuk meg, hogy
-n is átmenő kör. Mutassuk meg, hogy 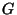 kétszeresen
pontösszefüggő.
kétszeresen
pontösszefüggő.
10. Határozzuk meg, hogy melyik az a legnagyobb 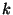 érték, amire
érték, amire
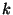 -szorosan pont-, illetve élösszefüggők az alábbi gráfok:
-szorosan pont-, illetve élösszefüggők az alábbi gráfok:
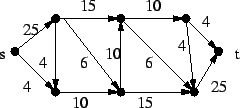
11. Adjunk meg az alábbi ábrán látható hálózatban egy maximális folyamot!
12. ZH Mutassuk meg, hogy egy 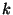 -szorosan összefüggo
-szorosan összefüggo
 -pontú gráfnak legalább
-pontú gráfnak legalább  éle van.
éle van.
13. (a) Mutassuk meg, hogy egy 2-reguláris gráf pont és
élösszefüggőségi szám megegyezik.
(b) Ugyanez 3-reguláris gráfokra.
14. ZH!, * Bizonyítsuk be, hogy ha 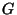 egy egyszerű síkgráf, akkor
egy egyszerű síkgráf, akkor 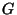 nem lehet
hatszorosan pontösszefüggő!
nem lehet
hatszorosan pontösszefüggő!
Csima Judit
2002-03-28