Bevezetés a számításelméletbe II.
2002. március 21.
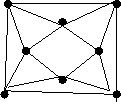
1. Perfekt-e az alábbi gráf?
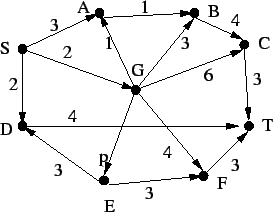
2. Állapítsuk meg, hogy mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Adjuk meg a kritikus utakat is!
3.
(a) Hány éle van a 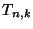 Turán-gráfnak, ha
Turán-gráfnak, ha  osztója
osztója 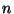 -nek?
-nek?
(b) Bizonyítsuk be, hogy a 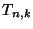 Turán-gráf minden
Turán-gráf minden 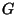 részgráfjára
részgráfjára 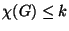 .
.
4. ZH! Egy legalább két csúcsú teljes gráf néhány, egy csúcshoz illeszkedő élét
elhagyjuk. Bizonyítsuk be, hogy az így kapott gráf perfekt.
5. ZH! Állapítsuk meg, hogy a 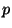 paraméter függvényében
mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Melyek a kritikus tevékenységek?
paraméter függvényében
mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Melyek a kritikus tevékenységek?
6. Mutass olyan 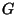 gráfot, amire
gráfot, amire
 , de
, de 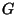 mégse perfekt!
mégse perfekt!
7. HF, ZH!
Egy 90 fős társaságból bizonyos párok leveleznek egymással. Akárhogyan
választunk ki közülük 10 embert, ezek között mindig van legalább kettő, akik
leveleznek egymással. Bizonyítsuk be, hogy a levelező párok száma legalább
405.
8. HF Adott egy 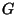 irányítatlan egyszerű gráf. Bizonyítsuk be, hogy
irányítatlan egyszerű gráf. Bizonyítsuk be, hogy 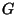 éleinek egy tetszoleges irányított kör mentes
irányításában az emeletek száma legalább
éleinek egy tetszoleges irányított kör mentes
irányításában az emeletek száma legalább 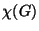 .
.
9. Bizonyítsuk be, hogy az 5 pontú teljes gráf élgráfja,
 nem perfekt!
nem perfekt!
10. ZH! Minimálisan hány éle kell, hogy legyen egy olyan 2000 csúcsú
egyszerű 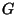 gráfnak, melyre
gráfnak, melyre 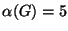 ?
?
11. ZH! Állapítsuk meg, hogy a 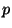 paraméter függvényében
mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Melyek a kritikus tevékenységek?
paraméter függvényében
mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Melyek a kritikus tevékenységek?
12. ZH! Bizonyítsuk be, hogy egy perfekt gráfból egy csúcs
megduplázásával nyert gráf is perfekt!
(A  csúcs megduplázása azt jelenti, hogy a
csúcs megduplázása azt jelenti, hogy a 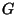 gráfhoz hozzáveszünk egy új
gráfhoz hozzáveszünk egy új 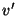 pontot, és azt a
pontot, és azt a  pont
pont
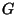 -beli szomszédaival kötjük össze.)
-beli szomszédaival kötjük össze.)
13. Legyen egy 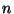 -elemu halmaz összes (azaz hány darab?)
részhalmaza egy
-elemu halmaz összes (azaz hány darab?)
részhalmaza egy  irányított gráf ponthalmaza, és az
irányított gráf ponthalmaza, és az  részhalmazának
megfelelo
részhalmazának
megfelelo
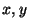 pontok között akkor és csak akkor vezessen él, ha
pontok között akkor és csak akkor vezessen él, ha
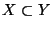 és
és
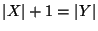 . Mutassuk meg, hogy
. Mutassuk meg, hogy 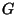 -ben nincs irányított kör, majd
adjuk meg mind maximális számú, mind minimális számú
emeletekre való bontását.
-ben nincs irányított kör, majd
adjuk meg mind maximális számú, mind minimális számú
emeletekre való bontását.
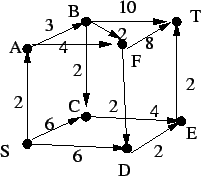
14. Állapítsuk meg, hogy mennyi a feladat elvégzéséhez minimálisan
szükséges idő az alábbi PERT diagram által leírt munkafolyamatnál!
Adjuk meg a kritikus tevékenységeket is!
15. Maximum hány éle lehet egy 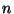 pontú, irányított kört
nem tartalmazó egyszeru gráfnak?
pontú, irányított kört
nem tartalmazó egyszeru gráfnak?
16.* Legyen 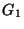 és
és 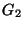 két olyan perfekt gráf, melyek metszete teljes gráf.
(A metszet pontjai a közos pontok, élei a közös élek.) Mutasd meg, hogy
két olyan perfekt gráf, melyek metszete teljes gráf.
(A metszet pontjai a közos pontok, élei a közös élek.) Mutasd meg, hogy
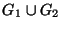 is perfekt! (Az únió pontjai a két ponthalmaz együtt,
élei az élhalmazok úniója.)
is perfekt! (Az únió pontjai a két ponthalmaz együtt,
élei az élhalmazok úniója.)
17. * Igazoljuk, hogy ha az 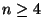 csúcsú egyszerű
csúcsú egyszerű 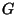 gráfnak
gráfnak
 éle van, akkor
éle van, akkor 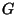 tartalmaz legalább két
(nem feltétlenül diszjunkt)
tartalmaz legalább két
(nem feltétlenül diszjunkt) 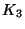 részgráfot.
részgráfot.
Csima Judit
2002-03-21