Bevezetés a számításelméletbe II.
2002. március 14.
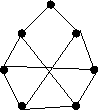
1. ZH! Mennyi az ábrán látható gráf élkromatikus száma?
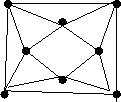
2. HF, Nem volt Perfekt-e az alábbi gráf?
3. Legyenek  csúcsai a sakktábla mezoi, és két csúcs pontosan
akkor legyen összekötve, ha a megfelelo mezok
bástyával egy lépésben elérhetok egymásból. Mennyi az
így keletkezett gráf kromatikus száma?
csúcsai a sakktábla mezoi, és két csúcs pontosan
akkor legyen összekötve, ha a megfelelo mezok
bástyával egy lépésben elérhetok egymásból. Mennyi az
így keletkezett gráf kromatikus száma?
4. ZH! Jelentse  a Mycielski konstrukcióval kapott azon gráfot, melynek
kromatikus száma
a Mycielski konstrukcióval kapott azon gráfot, melynek
kromatikus száma  . Adjuk meg az összes olyan
. Adjuk meg az összes olyan  értéket, melyre
értéket, melyre  tartalmaz Euler-kört!
tartalmaz Euler-kört!
* És Euler-út mikor van?
5. Bizonyítsuk be, hogy ha  egy
egy 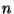 csúcsú egyszeru
reguláris gráf, akkor
csúcsú egyszeru
reguláris gráf, akkor
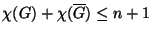 .
(
.
(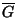 a
a  gráf komplementerét jelöli.)
gráf komplementerét jelöli.)
6. Nem volt Mutass olyan  gráfot, amire
gráfot, amire
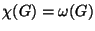 , de
, de  mégse perfekt!
mégse perfekt!
7. ZH! Mutasd meg, hogy minden egyszerű, síkba rajzolható 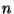 pontú gráfra
teljesül, hogy
pontú gráfra
teljesül, hogy
 .
.
8. HF, ZH! Legyen  egy
egy 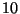 -reguláris egyszeru gráf, melynek
-reguláris egyszeru gráf, melynek 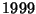 csúcsa
van. Mennyi a
csúcsa
van. Mennyi a  élkromatikus szám értéke?
élkromatikus szám értéke?
9. Nem volt, ZH! Egy legalább két csúcsú teljes gráf néhány, egy csúcshoz illeszkedő élét
elhagyjuk. Bizonyítsuk be, hogy az így kapott gráf perfekt.
10. ZH! Legyen  egy olyan egyszerű gráf, melynek pontjai számozhatók úgy, hogy
minden pont legfeljebb kettő nála nagyobb sorszámú ponttal van összekötve.
Mutasd meg, hogy
egy olyan egyszerű gráf, melynek pontjai számozhatók úgy, hogy
minden pont legfeljebb kettő nála nagyobb sorszámú ponttal van összekötve.
Mutasd meg, hogy  .
.
11. Nem volt Bizonyítsuk be, hogy az 5 pontú teljes gráf élgráfja,
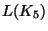 nem perfekt!
nem perfekt!
12. ZH! Legyen  a
a
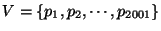 ponthalmazon
adott gráf, ahol
ponthalmazon
adott gráf, ahol
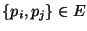 pontosan akkor, ha
pontosan akkor, ha  . Mennyi
. Mennyi
 élkromatikus száma, azaz
élkromatikus száma, azaz  ?
?
13. A 4. példában leírt gráfokban milyen  -ra van Hamilton kör?
-ra van Hamilton kör?
14. ZH!, * Mennyi
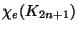 és
és
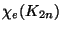 ?
?
15. Nem volt * Legyen 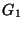 és
és 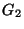 két olyan perfekt gráf, melyek metszete teljes gráf.
(A metszet pontjai a közos pontok, élei a közös élek.) Mutasd meg, hogy
két olyan perfekt gráf, melyek metszete teljes gráf.
(A metszet pontjai a közos pontok, élei a közös élek.) Mutasd meg, hogy
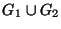 is perfekt! (Az únió pontjai a két ponthalmaz együtt,
élei az élhalmazok úniója.)
is perfekt! (Az únió pontjai a két ponthalmaz együtt,
élei az élhalmazok úniója.)
Csima Judit
2002-03-14