Bevezetés a számításelméletbe II.
2002. március 7.
1. ZH! Mennyi 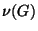 ,
, 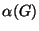 ,
, 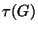 ,
, 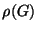 és
és 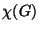 értéke a Petersen gráf esetén?
értéke a Petersen gráf esetén?
2. Mennyi 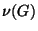 ,
, 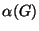 ,
, 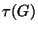 ,
, 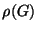 és
és 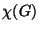 értéke a
értéke a  gráf esetén?
gráf esetén?
3. Az állatkertben nekünk kell megszervezni az éjjeliőrök
munkabeosztását, akiknek a lajhárra, az oroszlánra, a zebrára, a
csigára és a tigrisre kell vigyázniuk. Az Első Őr a reumája miatt nem
tud szaladni így csak a lajhárra vagy a csigára tud vigyázni.
A Második Őr ruhájához nem illik a csíkos minta, ezért ilyen állatot nem
hajlandó felügyelni. A Harmadik Őr ellenben csak csíkos állattal
hajlandó foglalkozni. A Negyedik Őr kedveli a kihívásokat,
ezért ő a tigrisre vagy az oroszlánra szeretne vigyázni.
Az Ötödik Őr a csigára nem akar vigyázni. A Hatodik Őr a lajhár, a
csiga, az oroszlán és a tigris kivételével bármit válal.
Minden őr egyszerre csak egy állatra tud vigyázni és még az is van,
hogy a tigrisre két embernek kell figyelnie.
Ki lehet-e osztani az őröket úgy, hogy a fenti feltételek teljesüljenek?
4. Egy egyszerű 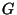 gráf csúcsainak száma 2000. Tudjuk továbbá, hogy
gráf csúcsainak száma 2000. Tudjuk továbbá, hogy
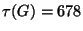 . Igazoljuk, hogy
. Igazoljuk, hogy 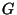 -ben nincs teljes párosítás!
-ben nincs teljes párosítás!
5. ZH! Legyenek a  gráf pontjai az
gráf pontjai az 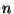 hosszú 0-1 sorozatok,
két pont akkor legyen összekötve, ha a nekik megfelelő sorozatok pontosan
egy helyen térnek el. Határozzuk meg
hosszú 0-1 sorozatok,
két pont akkor legyen összekötve, ha a nekik megfelelő sorozatok pontosan
egy helyen térnek el. Határozzuk meg
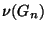 ,
, 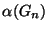 ,
,  ,
,  és
és  értékét
minden
értékét
minden 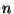 -re!
-re!
6. HF!!! ZH! A  csúcsú egyszeru
csúcsú egyszeru 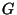 gráfban minden pont foka
legalább
gráfban minden pont foka
legalább 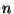 . Igazoljuk, hogy
. Igazoljuk, hogy 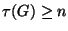 .
.
7. HF!!! Mutassuk meg, hogy egy 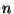 pontú, egyszerű
pontú, egyszerű 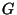 gráfban
gráfban
 .
.
8. HF!!! ZH! Legyen a 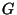 gráf ponthalmaza
gráf ponthalmaza
 és élhalmaza az
összes olyan
és élhalmaza az
összes olyan 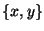 pár, ahol
pár, ahol 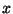 és
és 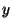 közül az egyik
osztója a másiknak. Határozzuk meg
közül az egyik
osztója a másiknak. Határozzuk meg 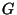 kromatikus számát!
kromatikus számát!
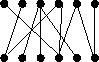
9. Keressünk maximális párosítást (persze mutassuk meg azt is, hogy
amit találtunk az az):
10. ZH! Legyen a 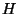 gráf csúcshalmaza
gráf csúcshalmaza
 és
két
és
két 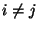 pont akkor legyen összekötve, ha
pont akkor legyen összekötve, ha 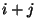 hárommal osztva 1 maradékot ad.
Határozzuk meg
hárommal osztva 1 maradékot ad.
Határozzuk meg
 ,
,  ,
,  ,
, 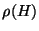 és
és 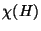 értékét!
értékét!
11. Az állatkertben szeretnénk az állatokat minél kevesebb cellába
elhelyezni. De a bárány fél a tigristől és az
oroszlántól, valamint a csiga fél, hogy
eltapossa a zebra. A medve és a tigris viszont
gusztustalannak tartja a csigát.
Továbbá a bagoly okoskodása idegesíti a zebrát, a medvét és a
bárányt, a medve horkolása viszont zavarja az oroszlánt.
Hány cellában tudjuk elhelyezni az állatokat, ha azt akarjuk,
hogy mindegyik jól érezze magát?
12. Legyen 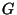 egy
egy  pontú gráf, mely egy
pontú gráf, mely egy  pontú
pontú  útból és egy
útból és egy 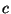 pontból áll, ami
pontból áll, ami  minden pontjával össze van kötve. Mennyi
minden pontjával össze van kötve. Mennyi 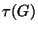 ?
?
13. Legyen 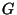 egy 100 csúcsú, egyszerű síkgráf komplementere. Mutassuk meg, hogy
egy 100 csúcsú, egyszerű síkgráf komplementere. Mutassuk meg, hogy
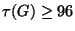 .
.
14. Határozzuk meg az
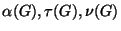 és
és 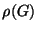 értékeket, ha
értékeket, ha
(a)  (teljes gráf), illetve
(teljes gráf), illetve
(b)  (
(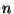 hosszú kör).
hosszú kör).
15. Mutassuk meg, hogy egy 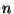 pontú, egyszerű
pontú, egyszerű 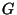 gráfban
gráfban
 .
.
16.* Tekintsünk a  véges csúcshalmazon két egyszerű gráfot,
véges csúcshalmazon két egyszerű gráfot,
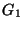 -et és
-et és 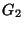 -t.
Jelölje
-t.
Jelölje 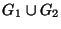 azt a gráfot
azt a gráfot  -n, melynek élhalmaza
-n, melynek élhalmaza
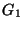 és
és 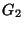 éleinek az uniója. Bizonyítsuk be, hogy
éleinek az uniója. Bizonyítsuk be, hogy
 .
.
17.*, ZH! Tekintsünk két véges, egyszerű gráfot 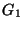 -et és
-et és 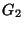 -t,
melyek kromatikus száma 3. Definiáljuk az
-t,
melyek kromatikus száma 3. Definiáljuk az 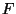 gráfot a következőképpen:
gráfot a következőképpen:
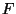 csúcsai az
csúcsai az  rendezett párok, ahol
rendezett párok, ahol 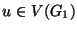 és
és 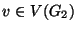 és
és
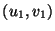 és
és 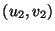 között akkor megy él,
ha
között akkor megy él,
ha 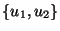 él
él 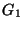 -ben és
-ben és 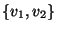 él
él 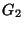 -ben. Mutassuk meg, hogy
-ben. Mutassuk meg, hogy
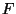 kromatikus száma is 3.
kromatikus száma is 3.
18. *, ZH! Legyen 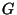 olyan véges, egyszerű gráf, melynek 1000 csúcsa
van és minden csúcs foka legalább 6. Igazoljuk, hogy
olyan véges, egyszerű gráf, melynek 1000 csúcsa
van és minden csúcs foka legalább 6. Igazoljuk, hogy 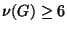 .
.
Csima Judit
2002-03-07