Bevezetés a számításelméletbe II.

2002. május 9.

1. Mutassuk meg, hogy 561 Carmichael-szám, vagyis összetett, de nincsen árulója. $(561=3 \cdot 11 \cdot 17)$

2. A XV. században is nagy hangsúlyt fektettek a biztonságos adatátvitelre, ezért minden király készíttetett magának egy lakatot egyetlen kulccsal. A titkos leveleket, kódexeket egy acél ládába tették, a biztonságos szállítás egyetlen módja a lelakatolt ládában történő továbbítás volt. Milyen eljárással küldhetett Mátyás király Artúr nevű kollégájának titkos üzenetet úgy, hogy saját kulcsát egyik sem adta ki a kezéből?

3. Határozzuk meg a dekódoló függvényt a 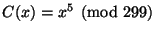$C(x)=x^5 \pmod{299}$ nyilvános kulcsú kódoláshoz!

4. Aliz és Béla telefonon keresztül sakkoznak. Ha a jatszma függőben marad, akkor az aki utoljára lépne, borítékolja ezt a lépését (ha nem így tenne, akkor a másiknak egy nap gondolkodási ideje lenne). Hogy lehet ezt telefonon át megtenni? (Például, ha Aliz borítékol, akkor Béla másnapig nem tudhatja, hogy Alíz mit lépett, Alíz viszont nem változtathatja meg lépését később.)