Bevezetés a számításelméletbe II.
2002. május 2.
1. Bizonyítsuk be, hogy a mod 6 maradékosztályok gyűrűt alkotnak a szokásos
mod 6 összeadással és szorzással. Egységelemes-e ez a gyűrű? Kommutatív-e?
2. Van-e nullosztó a  gyűrűben?
gyűrűben?
3. Mutassuk meg, hogy az  -es nem nulla determinánsú mátrixok
nem alkotnak ferdetestet a szokásos mátrixműveletekkel.
-es nem nulla determinánsú mátrixok
nem alkotnak ferdetestet a szokásos mátrixműveletekkel.
4. (a) Igaz-e, hogy ha 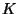 egy ferdetest. akkor nullosztómentes?
egy ferdetest. akkor nullosztómentes?
(b) Igaz-e fordítva, azaz, hogy ha egy 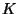 gyűrű nullosztómentes, akkor az
ferdetest?
gyűrű nullosztómentes, akkor az
ferdetest?
5. Melyik alkot gyurut, és melyik alkot testet? (Ha más nem
szerepel, akkor a két muvelet az összeadás és a szorzás.)
(a)
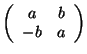 alakú mátrixok, ahol
alakú mátrixok, ahol
 ,
,
(b) egész együtthatós polinomok,
(c) a mod 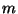 maradékosztályok a mod
maradékosztályok a mod 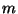 műveletekkel
műveletekkel
6. Egy 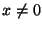 gyuruelem baloldali nullosztó, ha van olyan
gyuruelem baloldali nullosztó, ha van olyan
 , melyre
, melyre 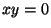 . Legyen
. Legyen 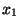 és
és 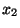 baloldali nullosztó.
Bizonyítsuk be, hogy
baloldali nullosztó.
Bizonyítsuk be, hogy 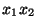 is baloldali nullosztó, de
is baloldali nullosztó, de  nem
feltétlenül az!
nem
feltétlenül az!
7. HF! Az ![$ [a,b]$](img14.gif) intervallumon folytonos függvények gyűrűt alkotnak-e az
összeadással és a szorzással? Egységelemes-e a gyűrű? Kommutatív-e?
Van-e benne nullosztó?
intervallumon folytonos függvények gyűrűt alkotnak-e az
összeadással és a szorzással? Egységelemes-e a gyűrű? Kommutatív-e?
Van-e benne nullosztó?
8. Igazoljuk, hogy ha egy testben 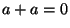 teljesül legalább egy
teljesül legalább egy
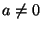 elemre, akkor minden elemre teljesül!
elemre, akkor minden elemre teljesül!
9. Gyurut vagy testet alkot
a
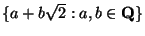 halmaz az összeadással és a szorzással?
halmaz az összeadással és a szorzással?
10. Legyen 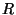 egy nullosztómentes gyuru. Bizonyítsuk be, hogy
egy nullosztómentes gyuru. Bizonyítsuk be, hogy
(a) ha egy  elemre
elemre 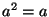 , akkor
, akkor 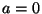 vagy
vagy 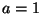 .
.
(b) ha egy  elemre
elemre 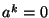 (egy
(egy 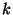 pozitív egészre), akkor
pozitív egészre), akkor 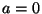 .
.
(c) Mutassuk meg, hogy nem nullosztómentes gyuruben a fentiek
nem igazak!
11. A mod 12 maradékosztályok gyűrűjében melyik elemeknek van inverze?
12. * Bizonyítsuk be, hogy kommutatív testben minden elemnek
legfeljebb két négyzetgyöke lehet. Igaz-e ez nem kommutatív testben?
Csima Judit
2002-05-02
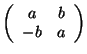 alakú mátrixok, ahol
alakú mátrixok, ahol