Bevezetés a számításelméletbe II.
2002. április 25.
1. Legyen  a komplex számok csoportja az összeadásra nézve,
a komplex számok csoportja az összeadásra nézve,
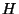 pedig a valósok csoportja az összeadásra nézve.
pedig a valósok csoportja az összeadásra nézve.
(a) Mutasd meg, hogy 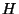 részcsoport
részcsoport  -ben.
-ben.
(b) Mik  -ben a
-ben a 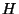 szerinti mellékosztályok?
szerinti mellékosztályok?
(c) Mutasd meg, hogy 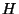 normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a
normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a  faktorcsoport.
faktorcsoport.
2. ZH! Egy csoport rendje  és van olyan eleme, melynek
és van olyan eleme, melynek 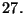 hatványa nem az egységelem. Bizonyítsuk be, hogy a csoport
kommutatív!
hatványa nem az egységelem. Bizonyítsuk be, hogy a csoport
kommutatív!
3. Jelentse 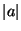 az
az  valós szám abszolút
értékét. Homomorfizmus-e az adott csoporton az
valós szám abszolút
értékét. Homomorfizmus-e az adott csoporton az
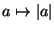 leképezés, ha
leképezés, ha
(a) a csoport a nem nulla valós számok a szorzásra nézve;
(b) a csoport a valós számok az összeadásra nézve?
Ha igen, mi lesz a leképezés képe és mi a magja, és mik
lesznek a mag szerinti mellékosztályok?
4. (a) Szorozzuk össze a két permutációt és az eredményt írjuk fel ciklikus módon:
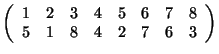
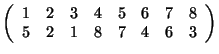 .
.
(b) Írjuk fel diszjunkt ciklusok szorzataként az alábbi
permutációt:
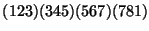 !
!
(c) Az  hetedfokú szimmetrikus csoport egy eleme az
hetedfokú szimmetrikus csoport egy eleme az  permutáció. Mi ennek az elemnek a rendje?
permutáció. Mi ennek az elemnek a rendje?
(d) Határozzuk meg az
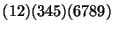 permutáció inverzét!
permutáció inverzét!
5. Legyen  a komplex számok csoportja a szorzásra nézve,
a komplex számok csoportja a szorzásra nézve,
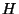 pedig az egységnyi abszolut értékű komplexek halmaza.
pedig az egységnyi abszolut értékű komplexek halmaza.
(a) Mutasd meg, hogy 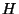 részcsoport
részcsoport  -ben.
-ben.
(b) Mik  -ben a
-ben a 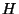 szerinti mellékosztályok?
szerinti mellékosztályok?
(c) Mutasd meg, hogy 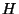 normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a
normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a  faktorcsoport.
faktorcsoport.
6. ZH! Tudjuk, hogy a  csoport rendje 100, a
csoport rendje 100, a 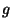 elemére pedig
teljesül, hogy
elemére pedig
teljesül, hogy 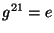 . Mit mondhatunk
. Mit mondhatunk 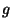 -rol?
-rol?
7. ZH! Legyen
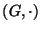 egy csoport és
egy csoport és 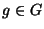 egy rögzített elem
egy rögzített elem  -ben.
Bizonyítsuk be, hogy a
-ben.
Bizonyítsuk be, hogy a
 leképezés homomorfizmus. Mi lesz
ennek a magja és képe?
leképezés homomorfizmus. Mi lesz
ennek a magja és képe?
8. ZH! A 2001 rendű  csoportnak
csoportnak 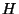 egy 69 rendű részcsoportja, ami
egyben normálosztó is. Bizonyítsuk be, hogy a
egy 69 rendű részcsoportja, ami
egyben normálosztó is. Bizonyítsuk be, hogy a  faktorcsoport kommutatív!
faktorcsoport kommutatív!
9. ZH! Bizonyítsuk be, hogy ha a  csoport rendje 55, akkor minden
csoport rendje 55, akkor minden
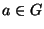 elemre teljesül, hogy az
elemre teljesül, hogy az  és az
és az  elemek rendje azonos.
elemek rendje azonos.
10. Bizonyítsd be, hogy egy ciklikus csoport minden részcsoportja is ciklikus.
11. Van-e az 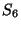 hatodfokú szimmetrikus csoportban kilencedrendu elem?
hatodfokú szimmetrikus csoportban kilencedrendu elem?
12. Legyen  az egész számok csoportja az összeadásra nézve,
az egész számok csoportja az összeadásra nézve,
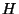 pedig a hárommal osztható egészek halmaza.
pedig a hárommal osztható egészek halmaza.
(a) Mutasd meg, hogy 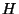 részcsoport
részcsoport  -ben.
-ben.
(b) Mik  -ben a
-ben a 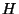 szerinti mellékosztályok?
szerinti mellékosztályok?
(c) Mutasd meg, hogy 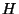 normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a
normálosztó is és határozd meg
hogy melyik ismert csoporttal izomorf a  faktorcsoport?
faktorcsoport?
13. ZH! Legyen  egy csoport, melynek rendje 55. Tudjuk még, hogy
egy csoport, melynek rendje 55. Tudjuk még, hogy
 -nek van legalább három különböző rendű eleme, melyek egyike sem az
egységelem. Bizonyítsuk be, hogy
-nek van legalább három különböző rendű eleme, melyek egyike sem az
egységelem. Bizonyítsuk be, hogy  kommutatív!
kommutatív!
14. Bizonyítsuk be, hogy kommutatív csoportban minden részcsoport
normálosztó!
15. ZH! Legyenek  és
és 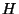 véges csoportok és
véges csoportok és 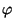 homomorfizmus
homomorfizmus
 -ből
-ből 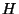 -ba. Bizonyítsuk be, hogy tetszőleges
-ba. Bizonyítsuk be, hogy tetszőleges 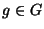 elemre a
elemre a 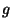 elem
rendje osztható a
elem
rendje osztható a
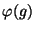 elem rendjével.
elem rendjével.
16. ZH! Legyen  egy 2001 rendű csoport és
egy 2001 rendű csoport és 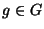 egy 23-rendű
eleme. Határozzuk meg
egy 23-rendű
eleme. Határozzuk meg 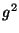 rendjét! (
rendjét! (
 )
)
17. Hány normálosztója van a 15 rendű ciklikus csoportnak?
18. * (a) Legyen  egy csoport, és
egy csoport, és  egy eleme. Igazoljuk, hogy
egy eleme. Igazoljuk, hogy 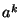 rendje, ahol
rendje, ahol 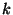 tetszoleges egész szám, osztója
tetszoleges egész szám, osztója  rendjének!
rendjének!
(b) Legyen  egy legalább kételemu véges csoport. Bizonyítsuk
be, hogy
egy legalább kételemu véges csoport. Bizonyítsuk
be, hogy  -nek van olyan eleme, melynek rendje prímszám!
-nek van olyan eleme, melynek rendje prímszám!
(c) Bizonyítsuk be, hogy ha egy csoportban minden egységelemtol
különbözo elem rendje ugyanaz, akkor ez az elem prím!
19. * Mely csoportokra lesz a
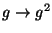 leképezés homomorfizmus?
leképezés homomorfizmus?
20. * Legyenek  és
és 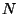 a
a  csoport normálosztói úgy, hogy közös
elemük csupán e
csoport normálosztói úgy, hogy közös
elemük csupán e  egységeleme. Lássuk be, hogy minden
egységeleme. Lássuk be, hogy minden 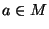 és
és  esetén
esetén  .
.
21. * Mutassunk példát olyan végtelen rendű csoportra, mely tetszőleges
véges számra tartalmaz 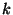 -ad rendű elemet!
-ad rendű elemet!
Csima Judit
2002-04-25
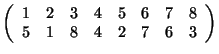
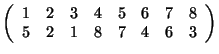 .
.