Megoldások a hetedik gyakorlathoz

1. A teljes feladatsorban szerepel a megoldás a Turing gépek 25. feladatnál.

2. Vegyük azt az M turing gépet, ami az y inputból előállítja x-et. Az x_f-et elő lehet állítani úgy, hogy ezen M turing gép után bekapcsolunk egy olyan M' gépet, ami minden inputra a szó fordítottját adja ki. Tehát így X_f megadható annyi bittel, amennyivel x plusz az M' Turing gép, ami konstans sok bit, azaz $C(x_f)\leq C(x)+c$. Fordítva érvelve, adódik, hogy x is megkapható annyi bitből, mint x, plusz konstans sok bit: $C(x)\leq C(x_f)+c$.

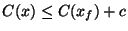3. Tetszőleges n-re vegyük a következő szót: x=1²ⁿ, azaz az a szó, ami 2ⁿ darab egyesből áll. Ennek hossz 2ⁿ, de megadható log₂n+c bittel, ami kisebb mint 0.5 log₂|x|=0.5 n.

4. A teljes feladatsorban szerepel a megoldás a Turing gépek 33. feladatnál.

5. A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok 1. feladatnál.

6. Először gondoljuk meg azt, hogy ha lenne egy olyan eljárásunk, ami egy részben kiszínezett gráfról eldönti, hogy lehet-e tovább folytatni a színezést úgy, hogy a végén jó 3-színezést kapjunk, akkor lenne polinomiális eljárás a színezésre. Ez a következő lenne: beszínezünk egy még nem színezett pontot valamelyik színnel és megkérdezzük az eljárást, hogy lehet-e folytatni ezt a színezést. Ha igen, akkor véglegesen olyan színűre festjük, ha nem, akkor másik színnel próbálkozunk. Ha a második szín se jó, akkor a harmadiknak már biztosan jónak kell lennie, mert mielőtt az új pont színezésébe kezdtünk volna, még lehetséges volt jó 3-színezést találni.
Most módosítsuk ezt a fenti dolgot úgy, hogy ne kelljen részben színezett gráfokkal dolgozni. Tegyük a következőt: vegyünk fel a G gráfon kívül 3 új pontot és ezeket kössük össze egymással minden lehetséges módon (3 új él). Ennek az új gráfnak (ami a G-ből áll meg ebből a hármas klikkből) pontosan akkor van jó 3 színezése, ha G-nek van. Ebben a jó 3-színezésben a hármas klikk pontjai különböző színeket kapnak, ezért beszélhetünk piros, kék és zöld új pontról. Ha most el karjuk dönteni hogy az eredeti G gráf egy pontja lehet-e piros egy jó 3-színezésben, akkor kössük össze a pontot az új pontok közül a kékkel és a zölddel és kérdezzük meg az eljárásunkat, hogy az így kapott gráf 3-színezhető-e. Ha igen, az azt jelenti, hogy a pont lehet piros, ha nem, akkor próbálkozunk másik színnel. Ezen eljárás költsége: konstans sok lépés az elején, majd minden pontnál max. 6 lépe's, beleértve az eljárás hívását is. Ez összesen is csak lineáris idő.

7.A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok 6. feladatnál.

8. A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok 17. feladatnál.

9. A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok 26. feladatnál.