


Next: About this document ...
Pótgyakorlat a hetedik gyakorlathoz
1. Igazoljuk, hogy a Karp redukció tranzitív, azaz: ha
 és
és
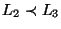 ,
akkor
,
akkor
 is fennáll!
is fennáll!
2. Igazoljuk, hogy a 4 színnel színezhető irányítatlan
gráfok nyelve NP-teljes!
3. Jelölje RH1 a részhalmaz-összeg probléma azon speciális esetét,
melyben az első súly 1 (a tanult jelöléssel: s1=1). Igazoljuk, hogy
az RH1 nyelv 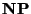 -teljes. (Ajánlás: adjunk meg egy
-teljes. (Ajánlás: adjunk meg egy
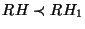 Karp-redukciót.)
Karp-redukciót.)
4. Igazoljuk, hogy a Hamilton-út probléma NP-teljes!
(Van-e G-ben
 élszámú egyszerű út?)
élszámú egyszerű út?)
5. Mutassuk meg, hogy a
 !
!
6. Igazoljuk, hogy a következő feladat P-beli:
Adott egy G gráf és egy
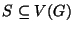 halmaz. Van-e G-nek olyan
feszítőfája, melynek végpontjai (elsőfokú pontjai) között S pontjai
mind szerepelnek?
halmaz. Van-e G-nek olyan
feszítőfája, melynek végpontjai (elsőfokú pontjai) között S pontjai
mind szerepelnek?
7. Igazoljuk, hogy a következő feladat NP-nehéz:
Adott egy G gráf és egy
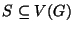 ponthalmaz. Van-e G-nek
olyan feszítőfája, melynek végpontjai pontosan az S pontjai?
ponthalmaz. Van-e G-nek
olyan feszítőfája, melynek végpontjai pontosan az S pontjai?
8. Jelölje H a következő hipotézist: Az NP-teljes feladatok nem oldhatók
meg O(1,2n)-nél kisebb lépésszámú algoritmussal, ahol n az input
mérete.
Mutassuk meg, hogy ha H igaz, akkor a következő feladat nem lehet
NP-teljes:
Input: Egy n csúcsú irányítatlan gráf G.
Kérdés: Van-e G -ben legalább 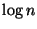 független pont?
független pont?
Pótgyakorlat a hetedik gyakorlathoz
1. Igazoljuk, hogy a Karp redukció tranzitív, azaz: ha
 és
és
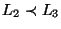 ,
akkor
,
akkor
 is fennáll!
is fennáll!
2. Igazoljuk, hogy a 4 színnel színezhető irányítatlan
gráfok nyelve NP-teljes!
3. Jelölje RH1 a részhalmaz-összeg probléma azon speciális esetét,
melyben az első súly 1 (a tanult jelöléssel: s1=1). Igazoljuk, hogy
az RH1 nyelv 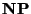 -teljes. (Ajánlás: adjunk meg egy
-teljes. (Ajánlás: adjunk meg egy
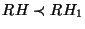 Karp-redukciót.)
Karp-redukciót.)
4. Igazoljuk, hogy a Hamilton-út probléma NP-teljes!
(Van-e G-ben
 élszámú egyszerű út?)
élszámú egyszerű út?)
5. Mutassuk meg, hogy a
 !
!
6. Igazoljuk, hogy a következő feladat P-beli:
Adott egy G gráf és egy
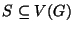 halmaz. Van-e G-nek olyan
feszítőfája, melynek végpontjai (elsőfokú pontjai) között S pontjai
mind szerepelnek?
halmaz. Van-e G-nek olyan
feszítőfája, melynek végpontjai (elsőfokú pontjai) között S pontjai
mind szerepelnek?
7. Igazoljuk, hogy a következő feladat NP-nehéz:
Adott egy G gráf és egy
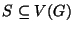 ponthalmaz. Van-e G-nek
olyan feszítőfája, melynek végpontjai pontosan az S pontjai?
ponthalmaz. Van-e G-nek
olyan feszítőfája, melynek végpontjai pontosan az S pontjai?
8. Jelölje H a következő hipotézist: Az NP-teljes feladatok nem oldhatók
meg O(1,2n)-nél kisebb lépésszámú algoritmussal, ahol n az input
mérete.
Mutassuk meg, hogy ha H igaz, akkor a következő feladat nem lehet
NP-teljes:
Input: Egy n csúcsú irányítatlan gráf G.
Kérdés: Van-e G -ben legalább 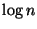 független pont?
független pont?



Next: About this document ...
Judit Csima
1999-12-16