Pikk Pakk játék tanuló gépi algoritmussal
Az oldal tartalma
A játék szabályai
A Pikk Pakk egy táblás játék amit 2 játékos játszhat egymás ellen. A táblán 49 golyó található, amelyből 24-24 az egyik illetve a másik jtátékoshoz tartozik egy pedig egy speciális golyó, a célgolyó. A játék folyamán a játékosok sorokat és oszlopokat tologatnak, arra törekedve, hogy a saját színükkel kerítsék be a célgolyót.
Az a teljes sor (oszlop) tolható el, egy lépésben mindig egy pozícióval, amelyben a lépő színe határozott többségben van.
Részletes szabályok:
Megállapodnak a játékosok a kezdőállás kialakításában. Ez történhet úgy, hogy nyitáskor csak egyetlen, a célgolyó, van a 9x9-es tábla közepén és a játékosok felváltva, egyenként tetszőlegesen választott helyre rakhatják le saját golyóikat (24 db-ot világos és 24 db-ot sötét) úgy, hogy a tábla szélső pozícióit üresen hagyják.
Ha bármelyik játékos kéri, akkor az ábrán mutatott állásból kell indítani a játékot, a világos kezdési jogával. Ha egyenkénti felrakással alakítják ki a nyitóállást, akkor sötét kezdi a lerakást és világos kezdi a tologatást.
A nyitóállásból kiindulva, az első lépésben a világos, azt a teljes sort (vagy oszlopot) tolhatja el egy pozícióval, amelyen többségben van. Sötét válaszlépése úgyszintén egy teljes sor (vagy oszlop) egy pozícióival történő elmozgatása, de ebben a sötét golyóknak kell többségben lenniük.
Újra világos, majd újra sötét és így tovább váltakozva következnek lépésre. Lépésenként mindig 7 db golyó mozgatható el, ha abban legalább 4 db golyó a lépő játékosé.
A partit az nyeri, aki a társát megelőzve keríti be a saját színével a célgolyót (azt négy oldaláról érintve, vízszintesen is és függőlegesen is).

Az ábrán mutatott állásban pl. sötét, a nyíllal jelölt sorban többségben van, így azt eltolhatja és nyer.
A tologatásoknak korlátot szab a játékmező határa, a parti végéig az összes golyó a táblán marad.
A tanuló algoritmus leírása
A számítógépes játékok fejlődése során kialakultak, az olyan logikai játékok ahol az ember már a gép ellen is tudott játszani. Ezekre a játékokra jellemző volt, hogy a játékos maga választotta ki, hogy a gép milyen szinten játszon. Ezek a szintek azonban statikusak voltak abban a tekintetben, hogy mindig egy megadott algoritmus szerint jászott egy adott szinten. Ez azt jelenti, hogy ha én ugyanúgy játszottam mindig, akkor ő is (persze az algoritmust ötvözhették egy kis véletlenszerűséggel, de lássuk, hogy ez az algoritmus "erőssége" szempontjából lényegtelen). Épp ezért ha már gyakran megverte az ember a gépet, akkor unalmassá vált a program, nem volt benne semmi kihívás.
A számítógépes hálózatok elterjedésével lehetővé vált az ember-ember elleni játék, ami már egy más szit, hiszen itt már nemcsak én hanem az ellenfél is fejlődhet a játék során. Az okos emberek azonban legyőzik a szerényebb képességüeket, így náluk felmerül az az kérdés, hogy: "Hogyan tudnék saját magam ellen játszani?"
Erre eszközt a Mesterséges Intelligencia szolgáltat. Különböző tanuló algoritmusokat alkalmazva lehet olyan gépi algoritmust írni, ami tanul ellenfelétől (vagy önmagától). Ez óriási előrelépés, hisz ez olyan mintha magam ellen játszanék, ugyanis ha sokat jászom az eleinte "üresfejű" géppel, akkor egy bizonyos idő után megtanulja a stratégiámat és ellenem alkalmazza, amire nekem a stratégiámat tovább kell fejlesztenem, amit, ha működik, ugyanúgy meg fog tanulni. Természetesen a tanító algoritmust tovább lehet fejleszteni, hogy a gép is képes legyen újabb, jobb stratégiákat kiépíteni.
A Pikk Pakk játékban is egy ilyen tanuló algoritmust alkalmazunk, a neve megerősítő tanulás (reinforcement learning). Ennek pontos leírása és matematikai háttere itt található. Az algoritmus lényege, hogy felépítünk egy stratégiai gráfot. Ennek a gráfnak a pontjai nem mások, mint a játék egyes állapotai (például.: kiinduló állapot, vagy ezen állapotból a 3. sor balra tólásával nyert új állapot), az élek pedig az egyes akciók amiknek következtében eljutunk az egyik állapotból a másik állapotba (akció például egy sor vagy oszlop tolása). Minden él az akció kódján kívül tartalmaz egy jósági értéket az úgynevezett q-értéket. Ez mutatja meg, hogy az adott akció mennyire jó. A mi esetünkben például ez az érték -1 és +1 között bármilyen értéket felvehet, a -1 azt jelenti, hogy ha ezt az akciót választod (az él kódjának megfelelő sor tolsz) akkor biztos veszteni fogsz, ha +1 akkor biztos nyerni. Minél nagyobb ez az érték annál kedvezőbb az élhez rendelt akciót választani. Innen már könnyü kitalálni, hogy a gép úgy fog játszani, hogy az adott állapotban mindig azt az akciót fogja válsztani, amelyik q-értéke a legnagyobb.
Kérdés még, hogy hogyan kaphatjuk meg ezt a stratégia gráfot és hogy hogyan bővíthető, illetve fejleszthető. Tegyük fel, hogy már van egy ilyen gráfunk. Játszunk egy játékot a játékossal a már meglévő stratégiafát használva. Ha olyan akciót hajt végre a játékos amivel még nem találkoztunk így benne sincs a stratégiafánkban akkor vegyünk fel egy új élet a megfelelő koddal és 0 q-értékkel. Ez jogos, hiszen a 0 q-érték egy semleges akcióra utal. Ha a játék során olyan állapottal találkozunk amivel még nem volt dolgunk akkor azt is vegyük bele a gráfba a megfelelő él (milyen akció végrehajtásával jutottunk ide) felvételével. A játék során rögzítsük a játék pontos menetét azaz, hogy melyik lépés után melyik jött. Ha a játék végetér, akkor magától értetődő, hogy az utolsó él q értéke 1-lesz, a többi él pedig megerősítő tanulásnál leírt súlymódosításnak megfelelően módosítjuk, azaz:
qúj(s,a) = -( r + ľ * max (q(s',a')) )
ahol r=0, ugyanis csak az utolsó lépéshez rendelünk hozzá jutalmat. A súlymódosítás fordított irányban végezzük el, mint ahogy a játék lefolyt, ezzel biztosítva, hogy a jutalom végigterjedjen a kiinduló állapotig.
Ha a fent leírt képletet figyelmesebben megnézzük, akkor észrevehetjük, hogy az eredeti megerősítő tanulásban nem ez a kifejezés szerepel az új q érték meghatározására, hanem ennek -1-szerese. Miért van itt így? Azért, mert míg a hagyományos megerősítő tanulásnál, a stratégiagráf egy ember (vagy robot) q értékeit írja le, a Pikk Pakk játékban a fent leirt módon készített gráf mind a két játékos (akik ráadásul egymás ellen, nem pedig egymást segítve) stratégáját tartalmazza. Gondoljuk meg, hogy ha egy játékos egy adott állapotban áll, akkor nem helyes azt az akciót válsztania, ami olyan új állapotban visz ahonnan a legjobb esély van a játék megnyerésére. Ez a lépés az ellenfél szempontjából a legjobb, tehát számomra a legrosszabb. Ezért kell -1-gyel szorozni a szomszéd legjobb akciójának q-értékét.
Ezzel az algoritmussal, tehát egyrészt bővítjük a stratégiafánkat, másrészt módosítjuk az éleken található q-értéket. A módszer akkor is alkalmazható, ha nics még ilyen stratégifánk (pontosabban a stratégiagráf csak a kiindulási állapotot tartalmazza 0 éllel), úgyanis ha egy olyan állapotban vagyunk amihez 0 él tartozik, úgyanis még nem volt ilyen állapot, akkor nézzük meg milyen akciókat választhatnánk elvileg, és sorsoljunk ki egyet ezek közül véletlenszerűen. Vegyük fel új élnek 0 q értékkel, miután a játék végetér úgyis módosulni fog pozitiv vagy negatív irányba attól függően, hogy ez a játékos nyert-e vagy az ellenfél.
Még egy kérdés felmerülhet, méghozzá az hogy mi van ha egy olyan állapotba jutunk, ahol már voltunk ebben a játékban, azaz hogyan kezeljük a hurkokat. Erre egy válasz lehet hogy ne foglalkozunk vele, hiszen a tanulóalgoritmusunra nincs hatással. Azonban ha jobban belegondolunk, akkor rájöhetünk, hogy egy él q értéke nagyban függ attól, hogy milyen távol van a célállapottól (azaz hány lépés kell innen a játék befejezéséhez). Ha egy lejátszott játékot úgy módosítunk, hogy beiktatunk egy hurkot, akkor a hurok előtti állapotoknak megváltozik a q értéke, közelebb kerül 0-hoz. Ha ugyanazt a hurkot még többször megismételjuk, akkor a hurok előtti állapotokat tovább semlegesítjük, hisz ez olyan mintha távolítanánk a végállapottól. Ez nem tűnik túl logikusnak, valahogy a játékot függetleníteni kellene a hurkoktól, azonban a hurok állapotait is kellene tanítani, hisz bármikor eljuthatunk ismét ezekbe az állapotokba. Ez a függetlenítés ebben a programban úgy került megoldásra, hogy a játék során a program folyamatosan figyeli az új állapotokat szerepeltek-e már a játékban, ha igen akkor ez egy hurok. A hurok állapotait tanítja a képletet alkalmazva, majd a hurkot kivágja, a játéklistából, mintha nem is járt volna ott. Ezzel a módszerrel a hurkok előtti állapotok függetlenek lettek a hurkoktól, és a hurkok állapotainak q értékeit sem "hanyagoltuk" el.
Az algoritmus konkrét megvalósítása
A Pikk Pakk játékot Java nyelven írtuk. Ennek a résznek az első felében csak a tanító algoritmus konkrét megvalósításáról írok, majd később részletezem a kliens szerver modelt és a grafikus felületet.
A tanító algoritmus szempontjából 3 osztályt kell kiemelni. A Gep osztály tartalmazza a stratégiafát, ami nem más mint egy Vector tipusú adatszerkezet. A sratégiafa csomópontokból és élekből áll. A mi programunkban az él a csomóponthoz tartozik (amelyikből kiindul), tehát a csomópont tagváltozója az éllista. A programban a csomópontot Valasztas-nak az él El-nek hívjuk. A stratégiafa tehát Valasztasok listája. Egy Valasztas pedig az állapotleíró tömbből és az éllistából áll. Az állapotleíró tömb egy 9*9-es byte típusú elemeket tartalmazó tömb, ami i-edik sorának j-edik eleme
- 0, ha a tábla i-edik sorának j-edik helyén nincs golyó
- 1, ha a kezdő játékos golyója található ott
- 2, ha a másik játékosé
- 3, ha a célgolyó.
Kevesebb memóriát használnánk fel ha ezeket az információkat 2 biten tárolni egy byte helyett (erre a Javaban lehetőség van).
Egy élt jellemez a q értéke, a végpontja (hogy a stratégiafa melyik csomopontjába mutat) továbbá az élkódja, ami azt mondja meg, hogy melyik sor/oszlop milyen irányú mozgatásához tartozik.
A fő osztályok fontosabb tagfüggvényeinek leírása.
A Gep osztály.
- public Gep(float gamma)
- Konstruktorában a megerősítő tanulás paraméterét a GAMMA-t kell megadni. A stratégiafa 0. eleme egy 0 egész értéket tartalmazó elem jelezvén hogy ez az elfogadó állapot. Ha egy él végpontja 0, akkor az azt jelenti, hogy vége a játéknak. A stratégiafa 1 állapota a kiindulóállapot.
- public void strategiakiir(String filename)
public void strategiabeolvas(String filename)
- A stratégiafát néha célszerű fájlba kiírni. hogy programleállás után ne kelljen az egész tanítást előről kezdeni. A kiírást és a beolvasást valósítja meg ez a két eljárás.
- public void egyeltanit(int valasztasszam,byte elszam)
- A stratégiafa egy élét tanítja a megerősítő tanulás alapján. Paraméterként a stratégiafa csomópontjának sorszámát, továbbá az itt talalható Valasztas élsorszámát kell megadni.
- void hurokkezel(Vector pontlista, Vector ellista,int ujpont)
- Egy játék során mindig rögzíteni kell annak menetét, hogy miután vége a játéknak tanítani tudjuk a jatékban résztvető éleket. A pontlista és azellista az aktuális játék során érintett csomópontokat és éleket tartalmazza. Ez a eljárás ellenőrzi, hogy az él amit felvenni készülünk ebbe a listába (azaz az akció amit lépünk) szerepel-e már benne, azaz a játék során voltunk-e már ugyanebben az állapotban. Amennyiben igen, az hurkot jelent, ami egyrészről tanítani kell, másrészről ki kell vágni a két listából.
- private boolean vege_e(byte [][] tempujval)
- Eldönti egy adott állásból, hogy nyert-e valaki. Paraméter a 9*9-es táblázatmátrix.
- private int sorszamotgeneral(byte [][] tempujval)
- Ez az eljárás eldönti, hogy a paraméterként kapott táblázattömb megegyezik-e a stratégiagráfunkban található Valasztas-ok valamelyikének táblázattömbjével. Amennyiben nem akkor felvesszük mint új állapot. A visszatérési érték Valasztas stratégiatömbben elfoglalt helye.
- public void partijatszik_tanit(boolean gepkezd_e)
- Ez az eljárás felelős egy teljes parti lebonyolításáért. Paraméterként az kell megadni, hogy ki kezd (ha a gép akkor TRUE-t kell átadni). Ő építi fel azt a két listát, ami tartalmazni fogja az aktuális játék éleit és csomópontjait, ő kéri be az adatokat, ő hívja meg a hurokkezel eljárást, és a játék végén ő tanítja az éleket a megfelelő sorrendben.
A Valasztas osztály
- public Valasztas(byte [][] allkod)
- Konstruktorában az állapotleíró tömböt kell megadni.
- public double maxq()
- A csomóponthoz tartozó élek q értékei közül a maximálisat adja vissza.
- public void legjobbel(newByte akcio,int ki)
- A csomóponthoz tartozó élek közül a legmagasabb q értékű él paramétereit fogják felvenni az eljárás paramétere.
- public boolean tolhat_e(byte elkod,int ki)
- Igaz értéket ad vissza ha a ki paraméterként megadott játékos (kezdő=1, ellenfele=2) tólhatja a paraméterként megkapott élhez tartozó sort vagy oszlopot.
- public void tol(byte elkod, byte[][] vegkod)
- Létrehoz egy új állapottáblát, ami az elkod paraméterként kapott élhez tartozó sor ill. oszlop mozgatásával jön létre.
- public void veletlenel(newByte elkod,int ki)
- Egy új véletlen élt sorsol azon élek közül amelyeket a ki paraméterű mozgathat.
- public boolean egyenlo_e(byte [][] masikkod)
- Megállapítja hogy a paraméterként kapott állapottábla azonos-e a Valasztas állapottáblájával.
- public void addEl(double q,byte elkod,int vegpont)
- Új él felvétele a Valasztas éllistájába.
Az El osztály
public El(double q,int vegpont, byte elkod)
-
- Konstruktorában az él q értékét, végpontjának sorszámát, továbbá az él kódját kell megadni kell megadni. Az él kódja:
- 0-8-ig balról az oszlopok felfelé húzása
- 9-17-ig fentről le a sorok jobbra tólása
- 18-26-ig balról az oszlopok lefelé tólása
- 27-35-ig fentről le a sorok balra húzása
Felhasználói felület működése
Az algoritmust implementáló program kliens-szerver alapú. A kliens egy Applet, aminek feladata, hogy megjelenítse a Pikk-Pakk játéktáblát és elküldje a játékos lépését a szervernek. Azért választottuk ezt a modellt, mert így a felhasználók bárhonnan játszhatnak a programmal egy Internet böngésző segítségével anélkül, hogy fel kellene installálniuk bármilyen programot. A Java nyelv kitűnően alkalmas Appleteket megvalósítására, továbbá kliens-szerver alapú kommunikáció támogatására.
- A kliens működése
A kliens elsődleges feladata, hogy megjelenítse a játéktáblát. A játéktábla 9x9-es méretű és 49 golyót tartalmaz. A golyók eltolása animálva történik, hogy élethű legyen a játék. Ilyenkor az adott sort ill. oszlopot pixelenként toljuk. Az egyes irányokba külön-külön függvény felel a tolásért. Ezen túl nyilvántartást is vezetünk a golyók helyzetéről. Erre azért van szükség, mert amikor a böngésző a háttérből újra látható lesz, automatikusan meghívódik az Applet paint() függvénye, amely újrarajzolja a tábla képét, és ehhez tudnunk kell a golyók elrendeződését.
Minden egyes sor és oszlop végén található egy gomb, ami a mozgatás irányát mutatja. Ha a felhasználó megnyom egy ilyen gombot, akkor a kliens elküldi a lépést a szervernek, ami kiértékeli és visszaküldi, hogy szabályos-e. Ez technikailag úgy került megoldásra, hogy a kliensben egy külön szál feladata, a beérkező üzenetek feldolgozása. A beérkező adat vagy egy sor ill. oszlop tolását, vagy a kezdő tábla rajzolását jelenti. Ez egy nagyon egyszerű protokoll, ami megkerüli, hogy a kliensnél állapotokat kelljen értelmezni, hiszen a kliens semmi mást nem tesz, csak elküldi a szervernek, hogy melyik lépést lépi a játékos. A szerver visszaküldi ugyan ezt a lépést (ha szabályos), amire a kiszolgáló szál - anélkül, hogy tudná, hogy ki lépte - meghívja a megfelelő toló függvényt. A szerver, miután visszaküldte a játékos lépését, elküldi a válaszlépést, amit a kiszolgáló rutin ugyancsak megjelenít. Ekkor a felhasználó látja, hogy a lépést elfogadták, és hogy a szerver mit válaszolt rá.
A kliens Appletet borland jbcl objektunokból építettük. Ez a visual nyelvekhez hasonló, kényelmes grafikus fejlesztői környezet. Hátránya hogy a nagyszámú nem standard Java könyvtár lényegesen meghosszabbítja a betöltés idejét.
A kliensnek a html oldalon kell megadni a szerver URL-jét és a port számot. Ez azért hasznos, mert így foglalt port estén vagy a szerver átköltöztetésénél ezek a paraméterek újrafordítás nélkül megváltoztathatóak.
- Szerver működése
A szerver létrehoz egy ServerSocket osztályt a program paramétereként kapott porton. Azaz a szervert java pikkpakk 5557 & paranccsal lehet elindítani, ahol az 5557 a port számot jelenti. Ha sikerült lefoglalni a portot, akkor egy végtelen ciklusban várja a kliens-kéréseket. Az új kliens számára létrehoz egy kiszolgáló szálat. Ez a kiszolgáló szál maga a tanító-játszó algoritmus (Gep class), ami várja a klienstől jövő lépéseket és visszaküldi a választ, majd a játék végén az új játék kódját. Először mindig a játékos kezd, majd a gép jön, és így tovább felváltva. A tanító játszó szál ezen kívül még képes detektálni a kapcsolat szétbomlását és a timeout elteltével befejezi futását, csökkentve ezzel a processzor terhelését. A program indításakor betölti a korábban kiírt döntési gráfot, amit minden tizedik játék (tanítás) után kiment fájlba.
A kiszolgáló szálak létrehozásával egyszerre több klienst is ki tud szolgálni a szerver.
Egyéb stratégiajavító ötletek és tudásbázis építő algoritmusok
Ha átgondoljuk, hogy hogyan teljesedik ki a stratégiafánk, akkor észrevehetjük, hogy ha egy állapotban már jártunk valamely játék során, azaz az állapothoz tartoznak élek, akkor a gép, mindig a legjobb akciót fogja kiválaszatni következő lépésnek. Ennek a legjobb akciónak a q értéke azonban lehet negativ, ami azt jelenti hogy ez a lépés nem jó. Gondoljuk meg, hogy van egy állapotunk, ahonnan 5 különböző állapotba juthatunk el, viszont a stratégiafánkban még csak egy állapot szerepel negatív q-értékkel. Ha egy játék során ismét eljutunk ide, akkor a gép ezt az élt fogja ismét választani, hisz a már ismert élek közül ez a legjobb választás, sőt akárhányszor jut ide mindig ezt fogjuk választani (egészen addig, míg egyszer a játékos kerül ide és ő egy másik akciót választ, ami következtében új élt veszünk fel a gráfban).
Ezt nem nevezhetjük túlzottan nagy hatásfokú tanulásnak. Ennek a problémának egy egyszerű kiküszöbölése lehet az alábbi megoldás: Ha a játék során olyan állapotba jutunk, ahonnak a legjobb él q értéke negatív, továbbá van legalább egy olyan él amit még nem vettünk fel a stratégiafánkba, akkor véletlenszerűen sorsoljunk ezek közül egyet, és azt az akciót lépjük meg. Látható, hogy ezzel a módosítással elértük, hogy a gépet nem lehet végtelensokszor ugyanazzal a lépéskombinációval megverni.
Amennyiben üres tudásbázisból indulunk ki, akkor meglehetősen sokat kell játszani ahhoz, hogy a gép eljusson egy olyan szintre, ahol már élvezhető vele a játék. Ezért felmerül annak az igénye, hogy már eleve rendelkezzen bizonyos tudással, ami persze később módosulhat. A következőkben leírok egy pár lehetőséget kezdő tudásbázis kialakítására. Kezdem a legegyszerűbbel, majd bemutatok egy pár apró fogást, amivel nagyban lehet növelni az alapverzió hatékonyságát.
Nyilván a legegyszerűbb megoldás, ha a gép önmagával játszik véletlenszerűen sok játékon kereszetül. Minden játék végén ugyanúgy módosítjuk a stratégiafa éleit mintha ember ellen játszanánk. Ha nagyon sokat játszik maga ellen a gép, akkor elvileg komoly tudásra tehet szert. Ez azonban csak elvileg van így. Miért? A 9*9 es Pikk Pakk esetén a lehetséges álapotok száma:
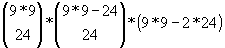
Valódi játék során azonban az állapottér csak egy töredékét járjuk be. Gondoljunk például arra ha a győzelem csak egy lépésre van, akkor a még kezdő játékos is megtalálja azt, nem pedig a másik 5-10 lehetőség közül fog játszani. Ha azonban két gép teljesen véletlenszerűen játszik, akkor ő nem ezt teszi, hanem "elkóborolnak" olyan állapotokba, ami nagy valószínűséggel sosem fog bekövetkezni. Tehát ez az alapmódszer csak óriási memória és rengeteg lehetséges tanulóidő mellett adhat hatékony eredményt. Ha ez nincs meg akkor kevés játék után is nagy állapotteret fog generálni viszont nagyon rosszul fog játszani.
Egy javítási lehetőség, hogy csak abban az esetben lép a gép véletlenszerűen, ha nem talál olyan élet, amit ha meglép akkor győz. Ennek a javított változatnak sokkal nagyobb a hatékonysága, és kisebb a memóriaigénye, hiszen ezzel az ellenőrzéssel fölösleges részgráfokat "vágunk le". Természetesen ezt tovább áltanánosíthatjuk és tehetünk olyan kitételeket, hogy ha viszont van olyan él, ami akcióját meglépve biztos az ellenfél győz, akkor ne ezt lépjük, pontosabban vegyük fel -1-es q értékkel, vagy mondhatjuk azt is hogy ha van olyan él amit ha meglépek akkor az ellenfél akármit lép nekem lesz olyan élem ami biztos győzelemre visz, akkor járjunk el hasonlóan, mintha ez a él olyan lenne, amit ha meglépünk biztos győzünk.
Ha már kialakult bizonyos tudásbázisunk, akkor célszerű, hogy ez egyik gép már a tanulóbázis alapján játszik és csak a másik véletlenszerűen. Természetesen ilyenkor partinként cseréljük, hogy ki az aki a már meglévő tudást felhasználja, a kezdő vagy aki másodszor lép. Igy nem fog az kialakulni, hogy a gép csak akkor tud jól játszani, ha ő kezd.