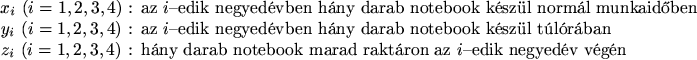
A megoldandó feladatokat először
a ???-i előadás szünetében lehet
átvenni.
Ha valaki nincs ott, akkor ettől az időponttól
fogva
bármikor megkeresheti Szeszlér Dávidot az IB 136/a
szobában. (A feladatot emailen elküldeni nem tudjuk;
kivétel
ez alól, ha valaki külföldön van, de
szeretné
teljesíteni a tárgyat.) A feladatok többsége
angol nyelvű, de a megoldás
természetesen
magyarul is beadható.
_KUKAC_cs.bme.hu
címre, de csak pdf,
vagy postscript
formátumban. (Így például a text, html, rtf
vagy winword dokumentum formátumban beküldött
megoldások
olvasatlanul töröltetnek.) A megoldásokon a
megoldó
nevén kívül a feladat
sorszámát,
és a megoldó email
elérhetőségét
is fel kell tüntetni. Kérjük szépen, hogy a
megoldást mindenki legkésőbb ???-ig
(aznap éjfélig) küldje el vagy adja le. A ???-i határidő után pár napon, de legkésőbb egy héten belül mindenki emailben kap értesítést arról, hogy a megoldás jó volt-e, vagy esetleg akad még rajta javítanivaló. (Ezen a héten kapnak értesítést azok is, akik a megoldást esetleg jóval a határidő előtt adták le.) Ha egy beadott megoldás nem tökéletes, akkor azon még lesz mód csiszolni, de kérjük szépen, hogy a javított megoldás is legkésőbb ???-ig érkezzen meg.
A beadandó feladat a
megoldótól
azt kívánja meg, hogy a feladatban
kitűzött
problémát megfogalmazza (formalizálja)
lineáris,
vagy egészértékű programozási
feladatként, ezt megoldja valamilyen LP/IP
megoldó
programmal, majd a kapott
megoldást az eredeti feladat
szövegének
megfelelően értelmezze. Az ingyenes LP/IP megoldó
programok közül ajánlható az LpSolve, amely
letölthető innen.
Mindez részletesen a
következőket
jelenti:
1. Mintafeladat
SilComputer needs to meet the demand of its largest corporate and educational customers for notebook computers over the next four quarters (before its current model becomes obsolete). SilComputer currently has 5,000 notebook computers in inventory. Expected demand over the next four quarters for its notebook is 7,000, 15,000, 10,000, and 8,000. SilComputer has sufficient capacity and material to produce up to 8,000 computers in each quarter at a cost of $2000 per notebook. By using overtime, up to an additional 2,000 computers can be produced at a cost of $2200 each. Computers produced in a quarter can be used either to meet that quarter's demand, or be held in inventory for use later. Each computer in inventory is charged $100 per quarter to reflect carrying costs. How should SilComputer meet its demand for notebooks at minimum cost?
Megoldás:
A cég költségeit három tényező befolyásolja: mennyi számítógépet készítenek az egyes negyedévekben normál munkaiőben, mennyit túlórában, illetve mennyi marad raktáron (inventory) az egyes negyedévek végén. Ennek megfelelően vezetjük be a feladat változóit:
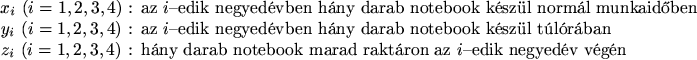
A feladat szövege szerint a cég költségeit kell minimalizálni. Ezért az alábbi célfüggvényt rendeljük a feladathoz (a szövegben található árak alapján):
![]()
Negyedévenként legföljebb 8000 notebook készülhet normál munkaidőben, illetve további legföljebb 2000 túlórában. Ezt fejezik ki az alábbi egyenlőtlenségek:

Az első negyedévben a kereslet várhatóan 7000 notebook, így a nomál munkaidőben és túlórában termelt mennyiség, valamint az eleve raktáron lévő mennyiség (5000 darab) összege el kell érje a 7000-et:
![]()
Az első negyedév végén megmaradó raktárkészlet a negyedévben megtermelt mennyiség és az előző raktárkészlet összege, mínusz az eladott 7000 darab:
![]()
A további három negyedévre is a fenti két egyenlőtlenségnek megfelelő egyenlőtlenségeket kell felírni: álljon rendelkezésre a keresletnek megfelelő mennyiség, illetve derüljön ki a negyedév végén megmaradó raktárkészlet.
2. negyedév:
Az összes bevezetett változónak egészértékűnek kell lenni (hiszen darabszámokat jelölnek). Ezzel a feladat egészértékű programozási megfogalmazása elkészült. Az LpSolve-val megoldva a következő megoldást kapjuk:

Ez tehát azt jelenti, hogy a SilComputer
akkor
jár a legjobban, ha mind a négy negyedévben 8000
darab
számítógépet állít elő
normál munkaidőben (vagyis a maximális
teljesítménnyel
dolgozik), emellett a második negyedévben 1000, a
harmadikban
2000 darabot termel túlórában. Ekkor egyedül
az első negyedév végén kell
raktároznia
6000 számítógépet. Az cég
költségei
így összesen 71,200,000 dollárt tesznek ki.
2. Mintafeladat
Coach Night is trying to choose the starting lineup
for
the basketball team. The team consists of seven players who have been
rated
(on a scale of 1=poor to 3=excellent) according to their ball-handling,
shooting, rebounding and defensive abilities. The positions that each
player
is allowed to play and the player's abilities are listed in the table
below.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The five-player starting lineup must satisfy the following restrictions:
1. At least 3 members must be able to play guard, at least 2 members must be able to play forward and at least 1 member must be able to play center.Given these constraints, Coach Night wants to maximize the total defensive ability of the starting team.2. The average ball-handling, shooting and rebounding level of the starting lineup must be at least 2.
3. If player 3 starts, then player 6 can not start.
4. If player 1 starts, then players 4 and 5 must both start.
5. Either player 2 or player 3 must start.
Megoldás.
A hét játékosról kell eldönteni, hogy bekerüljenek-e a kezdőcsapatba. Ezért mindegyikhez hozzárendelünk egy változót:
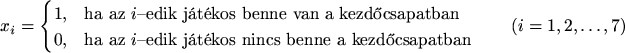
Az edző célja a védelem erejének, vagyis a kezdőcsapatba bekerülő játékosok védelemre kapott osztályzatai összegének maximalizálása, így az alábbi célfüggvényt rendeljük a feladathoz:
![]()
Az LP/IP megfogalmazásból természetesen következnie kell a változók 0-1 értékűségének, ezért minden változót egészértékűnek deklarálunk és felvesszük az alábbi egyenlőtlenségeket:

A kezdőcsapat 5 fős kell legyen, azaz:
![]()
A feladat 1-es feltétele szerint legalább 3 hátvéd, legalább 2 bedobó és legalább 1 center szerepre alkalmas játékos kell a kezdőcsapatba:

A 2-es feltétel szerint a kezdőcsapat labdakezelésre, lövésre, lepattanó megszerzésre kapott osztályzatainak átlaga legalább 2 kell legyen. Mivel a csapat 5 fős, ez azt jelenti, hogy az osztályzatok összege mindhárom esetben legalább 10:
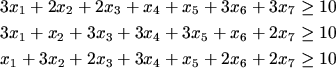
A 3-as feltétel szerint a 3-as és 6-os játékos egyszerre nem lehet benne a kezdőcsapatban:
![]()
A 4-es feltétel így fogalmazható meg:
![]()
Az 5-ös pedig így:
Ezzel a feladat egészértékű programozási megfogalmazása elkészült. Az LpSolve-val megoldva a következő megoldást kapjuk:

Ez tehát azt jelenti, hogy az (egyik lehetséges) optimális kezdőcsapatot az 1-es, 2-es, 4-es, 5-ös és 7-es játékosok alkotják. Ebben az esetben a védelemre kapott osztályzatok összege 9.