Bevezetés a számításelméletbe
II. Zárthelyi feladatok 2002.
május 24.
-
Bizonyítsuk be, hogy ha egy véges, hurokélmentes
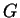 gráfnak van Euler-köre, akkor
gráfnak van Euler-köre, akkor 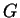 élgráfjának is van Euler-köre. Igaz-e az elobbi
állítás megfordítása?
élgráfjának is van Euler-köre. Igaz-e az elobbi
állítás megfordítása?
-
Bizonyítsuk be, hogy egy
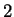 -reguláris
páros gráfban (tehát amiben minden fokszám
-reguláris
páros gráfban (tehát amiben minden fokszám 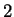 )
a különbözo teljes párosítások száma
mindig
)
a különbözo teljes párosítások száma
mindig 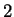 -nek
valamilyen pozitív egész kitevos hatványával
egyenlo.
-nek
valamilyen pozitív egész kitevos hatványával
egyenlo.
-
Mutassuk meg, hogy ha egy véges, egyszeru
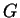 gráfra
gráfra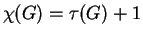 ,
akkor egyben
,
akkor egyben 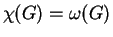 is teljesül.
is teljesül.
-
Mennyi az
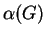 értéke egy olyan egyszeru
értéke egy olyan egyszeru 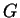 gráfra, aminek
gráfra, aminek 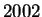 csúcsa van, és éleinek száma a leheto legnagyobb
azon feltétel mellett, hogy nem tartalmaz
csúcsa van, és éleinek száma a leheto legnagyobb
azon feltétel mellett, hogy nem tartalmaz 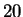 -nál
nagyobb klikket.
-nál
nagyobb klikket.
-
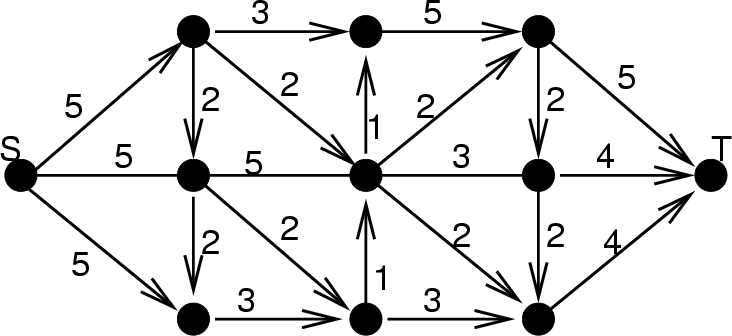
Adjunk meg egy maximális folyamot és állapítsuk
meg annak értékét az alábbi hálózatban!
(Az élekre írt számok a kapacitásokat jelentik.)
-
Legyen
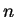 olyan pozitív egész szám, ami sem
olyan pozitív egész szám, ami sem 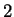 -vel,
sem
-vel,
sem 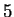 -tel
nem osztható. Bizonyítsuk be, hogy ekkor létezik olyan
-tel
nem osztható. Bizonyítsuk be, hogy ekkor létezik olyan 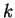 pozitív egész, amire
pozitív egész, amire 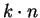 tízes számrendszerbeli alakja csupa
tízes számrendszerbeli alakja csupa 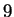 -es
számjeggyel írható le.
-es
számjeggyel írható le.
-
Oldjuk meg az alábbi kongruenciát (vagyis állapítsuk
meg az azt kielégíto
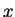 (-ek)
68-cal adott maradékát)!
(-ek)
68-cal adott maradékát)!
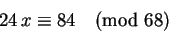
-
Legyenek
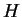 és
és 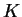 egy
egy 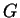 csoport részcsoportjai. Bizonyítsuk be, hogy ha
csoport részcsoportjai. Bizonyítsuk be, hogy ha 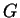 -nek
a részhalmazszorzással (komplexusszorzással) létrejövo
-nek
a részhalmazszorzással (komplexusszorzással) létrejövo 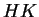 és
és 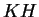 részhalmazai azonosak, vagyis
részhalmazai azonosak, vagyis 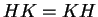 ,
akkor
,
akkor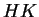 is részcsoportja
is részcsoportja 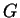 -nek.
-nek.
A feladatok sorrendje nem jelent nehézségi sorrendet.
Minden feladat 10 pontot ér. Az elégséges eléréséhez
szükséges minimális pontszám 32.
Puszta (indoklás nélküli) eredményközlésért
nem jár pont.
A dolgozatra kérjük jól olvashatóan
felírni a következo adatokat: név, neptun-kód,
tankör száma, gyakorlatvezeto neve.
Bevezetés a számításelméletbe II.
Zárthelyi feladatok 2002. június 4.
-
Legyen
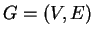 véges, összefüggo gráf. Mutassuk meg, hogy
véges, összefüggo gráf. Mutassuk meg, hogy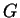 -ben
megadható olyan minden élen áthaladó séta,
amely minden élen legfeljebb kétszer halad át.
-ben
megadható olyan minden élen áthaladó séta,
amely minden élen legfeljebb kétszer halad át.
-
Legyen
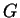 olyan
olyan 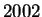 csúcsú gráf, aminek van Hamilton-köre. Mutassuk
meg, hogy ha
csúcsú gráf, aminek van Hamilton-köre. Mutassuk
meg, hogy ha 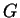 -bol
elhagyunk
-bol
elhagyunk 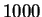 csúcsot (a hozzájuk csatlakozó élekkel együtt),
akkor a megmaradó gráfnak még mindig van legalább
két éle.
csúcsot (a hozzájuk csatlakozó élekkel együtt),
akkor a megmaradó gráfnak még mindig van legalább
két éle.
-
Legyenek egy
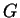 gráf csúcsai azok a
gráf csúcsai azok a 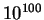 -nál
nem nagyobb pozitív egész számok, amelyeknek van
-nál
nem nagyobb pozitív egész számok, amelyeknek van 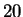 -nál
kisebb prímosztója.
-nál
kisebb prímosztója. 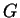 két csúcsa pontosan akkor alkot élet, ha a megfelelo
pozitív egészek relatív prímek. Állapítsuk
meg
két csúcsa pontosan akkor alkot élet, ha a megfelelo
pozitív egészek relatív prímek. Állapítsuk
meg 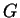 kromatikus számának értékét!
kromatikus számának értékét!
-
Legyen
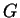 olyan
olyan 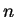 csúcsú véges egyszeru gráf, amelyik nem perfekt,
de ha tetszoleges csúcsát elhagyjuk, az így kapott
gráf már perfekt. Mutassuk meg, hogy
csúcsú véges egyszeru gráf, amelyik nem perfekt,
de ha tetszoleges csúcsát elhagyjuk, az így kapott
gráf már perfekt. Mutassuk meg, hogy 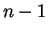 nem lehet prímszám.
nem lehet prímszám.
-
Állapítsuk meg a feladat elvégzéséhez
szükséges ido hosszát és határozzuk meg
a kritikus utakat az alábbi PERT diagramon! (Az élekre írt
számok az adott élek ``hosszát'' jelentik.)

-
Mutassuk meg, hogy
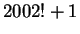 osztható
osztható 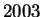 -mal
-mal
-
Oldjuk meg az alábbi kongruenciát (vagyis állapítsuk
meg az azt kielégíto
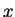 (-ek)
77-tel adott maradékát)!
(-ek)
77-tel adott maradékát)!
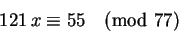
-
Legyen
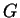 csoport,
csoport, 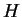 és
és 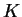 pedig
pedig 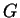 -nek
részcsoportjai. Mutassuk meg, hogy
-nek
részcsoportjai. Mutassuk meg, hogy 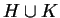 akkor és csak akkor részcsoportja
akkor és csak akkor részcsoportja 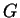 -nek,
ha vagy
-nek,
ha vagy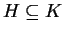 ,
vagy
,
vagy 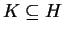 .
.
A feladatok sorrendje nem jelent nehézségi sorrendet.
Minden feladat 10 pontot ér. Az elégséges eléréséhez
szükséges minimális pontszám 32.
Puszta (indoklás nélküli) eredményközlésért
nem jár pont.
A dolgozatra kérjük jól olvashatóan
felírni a következo adatokat: név, neptun-kód,
tankör száma, gyakorlatvezeto neve.
