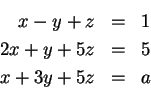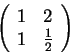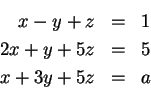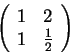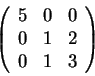Zárthelyi feladatok 1999. november 4.
- Határozzuk meg az alábbi egyenletrendszer megoldásait az
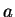 paraméter függvényében!
paraméter függvényében!
- Határozzuk meg az
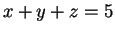 egyenletű sík
és a
egyenletű sík
és a
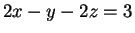 egyenletű sík metszésvonalának
azt a pontját, amelyik az
egyenletű sík metszésvonalának
azt a pontját, amelyik az 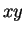 síkba (vagyis az
síkba (vagyis az 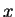 tengely és
az
tengely és
az 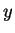 tengely által meghatározott síkba) esik!
tengely által meghatározott síkba) esik!
- Az
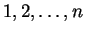 számok tetszőleges
számok tetszőleges 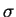 permutációjához
rendeljük hozzá a
permutációjához
rendeljük hozzá a 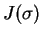 számot, ami a
számot, ami a
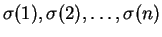 sorozatban azon elempárok
száma, melyek nem állnak inverzióban egymással.
Továbbá jelölje
sorozatban azon elempárok
száma, melyek nem állnak inverzióban egymással.
Továbbá jelölje 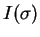 a
a 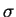 permutáció inverzióinak
a számát.
Mely
permutáció inverzióinak
a számát.
Mely 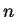 -ekre létezik olyan
-ekre létezik olyan 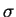 permutáció, hogy
permutáció, hogy
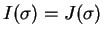 ?
?
- Az
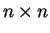 -es
-es 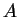 mátrix minden eleme páros szám.
Tudjuk, hogy
mátrix minden eleme páros szám.
Tudjuk, hogy 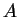 determinánsa osztható 64-gyel, de nem osztható
128-cal. Adjuk meg
determinánsa osztható 64-gyel, de nem osztható
128-cal. Adjuk meg 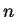 összes lehetséges értékét!
összes lehetséges értékét!
- Határozzuk meg az alábbi mátrix inverzét!
- Legyen
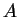 egy
egy 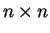 -es invertálható mátrix,
-es invertálható mátrix, 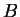 pedig egy
olyan
pedig egy
olyan 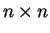 -es mátrix, amelyre
-es mátrix, amelyre
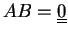 .
Igazoljuk, hogy ekkor
.
Igazoljuk, hogy ekkor
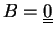 .
(Itt
.
(Itt
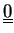 azt a mátrixot jelöli, amelynek minden eleme 0.)
azt a mátrixot jelöli, amelynek minden eleme 0.)
- A
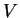 vektortér két alterének,
vektortér két alterének, 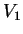 -nek és
-nek és 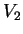 -nek
a nullvektor az egyetlen közös eleme. Bizonyítsuk be, hogy
-nek
a nullvektor az egyetlen közös eleme. Bizonyítsuk be, hogy
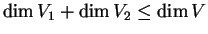 .
.
- Két játékos A és B egy kétszer kettes tábla
mezőibe felváltva ír be valós számokat, amelyek egyike sem
lehet nulla.
Az A játékos célja, hogy a kialakuló
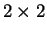 -es
-es
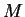 mátrix rangja 1 legyen, B pedig azt szeretné elérni,
hogy
mátrix rangja 1 legyen, B pedig azt szeretné elérni,
hogy 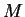 rangja legyen 2.
Tételezzük fel, hogy A is és B is a lehető
legjobban játszik.
Ki fog nyerni, ha A kezdi a játékot, és ki fog nyerni, ha
B kezd?
rangja legyen 2.
Tételezzük fel, hogy A is és B is a lehető
legjobban játszik.
Ki fog nyerni, ha A kezdi a játékot, és ki fog nyerni, ha
B kezd?
Zárthelyi feladatok 1999. december 9.
- Oldjuk meg az alábbi egyenletet a komplex számok körében!
(A
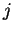 a képzetes egységet jelöli.)
a képzetes egységet jelöli.)
- Mi a primitív tizenkettedik egységgyökök összege?
- Mik a sajátértékei az alábbi mátrixnak?
- Bizonyítsuk be, hogy ha az
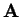 invertálható mátrixnak
sajátértéke a
invertálható mátrixnak
sajátértéke a 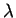 valós szám, akkor
valós szám, akkor 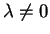 és
az
és
az 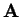 mátrix
mátrix 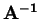 inverzének sajátértéke lesz az
inverzének sajátértéke lesz az
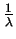 szám.
szám.
- Legyen az
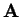 mátrix az
mátrix az 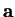 oszlopvektor szorzata a
transzponáltjával, azaz a vele azonos koordinátákkal bíró
oszlopvektor szorzata a
transzponáltjával, azaz a vele azonos koordinátákkal bíró 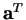 sorvektorral. (Tehát az
sorvektorral. (Tehát az 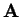 mátrix
mátrix 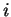 -edik sorának
-edik sorának 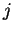 -edik
eleme az
-edik
eleme az 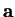 vektor
vektor 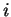 -edik és
-edik és 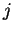 -edik koordinátájának
szorzata.) Bizonyítsuk be, hogy
-edik koordinátájának
szorzata.) Bizonyítsuk be, hogy 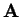 pozitív szemidefinit
mátrix!
pozitív szemidefinit
mátrix!
- Mi a számossága annak a számhalmaznak, melynek elemei azok a számok,
melyek felírhatók
 alakban úgy, hogy
alakban úgy, hogy 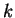 pozitív egész,
pozitív egész,
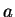 és
és 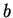 pedig racionális számok?
pedig racionális számok?
- Nyolc ember szeretne teniszezni három teniszpályán úgy, hogy az egyik
pályán párost, a két másikon egyénit
játszanak. Hányféleképpen tehetik ezt meg, ha a pályákat
különbözőeknek tekintjük, de ugyanazon pálya két
térfelét nem különböztetjük meg? (Természetesen az embereket is
különbözoeknek tekintjük, és az is számít, hogy
a négy páros meccset játszó játékos között ki kinek a partnere.)
- Hány különböző olyan körmentes gráf létezik
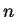 cimkézett ponton,
amelyben az élek száma valamilyen
cimkézett ponton,
amelyben az élek száma valamilyen 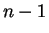 -nél kisebb fix
-nél kisebb fix 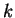 szám
és amiben pontosan
szám
és amiben pontosan 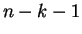 izolált pont van? (Egy csúcsot izolált
pontnak nevezünk, ha egyetlen él sem indul ki belőle.)
izolált pont van? (Egy csúcsot izolált
pontnak nevezünk, ha egyetlen él sem indul ki belőle.)