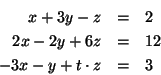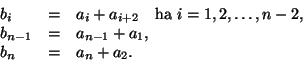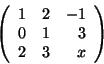Bevezetés a számításelméletbe I.
Zárthelyi feladatok
2000. november 2.
- Adjuk meg, az
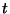 paraméter értékétől függően,
az alábbi egyenletrendszer megoldását.
paraméter értékétől függően,
az alábbi egyenletrendszer megoldását.
- Határozzuk meg a 3 dimenziós térben az
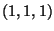 és
és 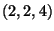 pontokon átmenő egyenesnek és a
pontokon átmenő egyenesnek és a 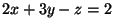 egyenletű síknak
a metszetét.
egyenletű síknak
a metszetét.
- Mely
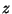 komplex számokra teljesül a
komplex számokra teljesül a
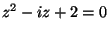 egyenlet?
egyenlet?
- Mi a
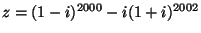 komplex szám kanonikus alakja?
komplex szám kanonikus alakja?
- Legyen
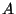 egy
egy 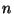 sorból és
sorból és 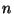 oszlopból álló valós mátrix,
a
oszlopból álló valós mátrix,
a 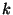 -adik sorának
-adik sorának 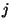 -edik elemét jelölje
-edik elemét jelölje 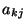 .
Legyen
.
Legyen 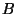 az az
az az 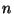 -szer
-szer 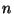 -es mátrix, amiben a
-es mátrix, amiben a 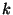 -adik sor
-adik sor
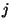 -edik eleme
-edik eleme
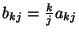 (
(
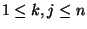 ).
Mennyi
).
Mennyi 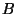 determinánsa, ha tudjuk, hogy
determinánsa, ha tudjuk, hogy 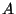 determinánsa 1?
determinánsa 1?
- A valós számhármasok vektorterében
alteret alkotnak-e azok az
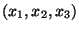 vektorok, melyekre
vektorok, melyekre
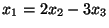 ?
?
- Legyen a
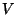 térnek
térnek
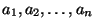 egy bázisa.
Tekintsük a következő
egy bázisa.
Tekintsük a következő 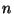 vektort:
vektort:
(a) 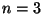 esetén bázist alkotnak-e a
esetén bázist alkotnak-e a
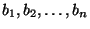 vektorok?
vektorok?
(b) 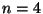 esetén bázist alkotnak-e?
esetén bázist alkotnak-e?
(Szorgalmi feladat: általában 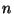 -re bázist alkotnak-e ? )
-re bázist alkotnak-e ? )
- Legyen
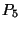 a legfeljebb ötödfokú valós együtthatós polinomok tere.
Vegyük azt az
a legfeljebb ötödfokú valós együtthatós polinomok tere.
Vegyük azt az
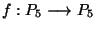 leképezést, melynél
leképezést, melynél
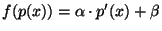 valamely rögzített
valamely rögzített
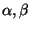 valós számokra.
Határozzuk meg az összes olyan
valós számokra.
Határozzuk meg az összes olyan 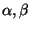 párt, amire
az
párt, amire
az 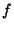 leképezés lineáris lesz. Ha
leképezés lineáris lesz. Ha 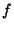 lineáris leképezés, adjuk meg
egy mátrixát is.
lineáris leképezés, adjuk meg
egy mátrixát is.
Bevezetés a számításelméletbe I.
Zárthelyi feladatok
2000. december 7.
- Határozzuk meg
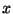 minden értékére az
minden értékére az
mátrix rangját!
- Egy
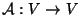 lineáris transzformációt
tükrözésnek hívunk, ha minden
lineáris transzformációt
tükrözésnek hívunk, ha minden 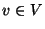 vektorra
vektorra
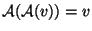 .
Bizonyítsuk be, hogy tükrözés mátrixának determinánsa
nem lehet 0.
.
Bizonyítsuk be, hogy tükrözés mátrixának determinánsa
nem lehet 0.
- Az
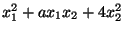 kvadratikus alak az
kvadratikus alak az 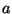 paraméter
értékétől függően mikor milyen definit lesz?
paraméter
értékétől függően mikor milyen definit lesz?
- Bontsuk a sík összes egyeneseinek halmazát két részhalmazra:
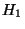 -et alkossák az origón átmenő egyenesek,
-et alkossák az origón átmenő egyenesek, 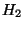 -t a többi.
Határozzuk meg
-t a többi.
Határozzuk meg 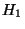 és
és 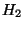 számosságát!
számosságát!
- Tíz gyerek hányféleképpen állítható úgy sorba,
hogy Jancsi és Juliska egymás mellett álljanak?
- Rajzoljuk le azt a gráfot, melynek pontjai a 4 hosszú
nullákból és egyesekből álló sorozatok és
két csúcs akkor van éllel összekötve, ha
egyik a másikból egy ``forgatással'' megkapható,
azaz ha az egyik a
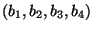 akkor a másik a
akkor a másik a
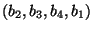 sorozathoz
tartozó pont.
sorozathoz
tartozó pont.
- Hány olyan páronként nem izomorf 6 pontú összefüggő
egyszerű gráf létezik, melyben két másodfokú és
négy harmadfokú pont van?
- Az előre megszámozott (címkézett)
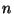 darab pont közé
hányféleképp húzhatunk be éleket úgy, hogy egyszerű
gráfhoz jussunk?
darab pont közé
hányféleképp húzhatunk be éleket úgy, hogy egyszerű
gráfhoz jussunk?