By a DNA-like alphabet we mean an alphabet of ![]() symbols,
symbols, ![]() ,
in the following form:
,
in the following form:
![]() . We say that letters
. We say that letters ![]() and
and
![]() are
complementary letters and we call
are
complementary letters and we call
![]() the alphabet
of purines of
the alphabet
of purines of ![]() and
and
![]() is said to be the alphabet
of pyrimidines of
is said to be the alphabet
of pyrimidines of ![]()
The complementary word of a string ![]() in
in ![]() is obtained by replacing each
letter in
is obtained by replacing each
letter in ![]() with its complementary letter and it is denoted by
with its complementary letter and it is denoted by
![]() The complementary word of the empty word is itself.
The morphism
The complementary word of the empty word is itself.
The morphism ![]() , which
assigns to each
word
, which
assigns to each
word ![]() its complementary word,
its complementary word,
![]() is called the Watson-Crick
morphism.
is called the Watson-Crick
morphism.
A standard Watson-Crick ET0L system is a construct
![]() with the following properties.
with the following properties.
![]() is a DNA-like
alphabet,
is a DNA-like
alphabet,
![]()
![]() is a finite set of tables over
is a finite set of tables over ![]() , where each table
, where each table ![]()
![]() is a complete set of context-free rules over
is a complete set of context-free rules over ![]() ,
,
![]() is the axiom
(with
is the axiom
(with
![]() ), and
), and
![]() is a non-empty subset of
is a non-empty subset of ![]() , the
terminal alphabet of the system.
, the
terminal alphabet of the system.
The derivation step in a standard Watson-Crick ET0L system
![]() is
defined as follows.
For two words,
is
defined as follows.
For two words,
![]() and
and
![]() ,
where
,
where ![]() ,
,
![]() ,
,
![]() we say that
we say that ![]() directly derives
directly derives
![]() in
in ![]() written as
written as
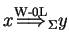 , if the following holds:
for some
, if the following holds:
for some ![]()
![]()
![]() for every
for every
![]() and
furthermore, if
and
furthermore, if
![]() , then
, then ![]() for every
for every
![]() and
and
![]() for every
for every
![]() otherwise.
In the latter case we say that a complementary transition takes place.
otherwise.
In the latter case we say that a complementary transition takes place.
Thus, if in the string obtained by parallel derivation there are not more pyrimidines than purines, then the derivation continues in the usual manner, like in the case of ET0L systems. Otherwise, if the pyrimidines are in a strict majority in the word, then the derivation continues from the complementary word of the generated string.
We denote the
transitive and reflexive closure of
![]() by
by
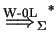 .
The generated language consists of those words over
.
The generated language consists of those words over
![]() which can be obtained from the axiom in some derivation steps:
which can be obtained from the axiom in some derivation steps:

If ![]() , that is, if there is only one table, then the system is
called a standard Watson-Crick E0L system.
In this case we use the notation
, that is, if there is only one table, then the system is
called a standard Watson-Crick E0L system.
In this case we use the notation
![]() , for
, for ![]() being the unique table of the system.
being the unique table of the system.
If all the tables are deterministic, that is, there is exactly one rule for each letter in each table, then the system is called a standard Watson-Crick EDT0L system.
Now we present an example which illustrates the generative power of standard Watson-Crick Lindenmayer systems and shows how these systems work.
In this example we have a standard Watson-Crick
E0L system and we generate the language (the same as in Example 5.10)
![]() , which is known not to be in ET0L
(see [Rozenberg and SalomaaRozenberg and
Salomaa1980]).
, which is known not to be in ET0L
(see [Rozenberg and SalomaaRozenberg and
Salomaa1980]).
The form of the rules for the remaining letters of the alphabet
(i.e. the ones not mentioned in ![]() ) is not important because these
letters never occur in any derivation, but in order to have a
complete table we also put the rules
) is not important because these
letters never occur in any derivation, but in order to have a
complete table we also put the rules
![]() into
into ![]() , for each
letter
, for each
letter ![]() not mentioned above.
not mentioned above.
Now we explain how this standard Watson-Crick E0L system works.
First the system uses the rules
![]() and derives a word in the form of
and derives a word in the form of
![]() , where
, where ![]() .
If in the next step the system uses the rule
.
If in the next step the system uses the rule
![]() instead of the rule
instead of the rule
![]() , then there will be more
pyrimidines
than purines in the sentential form, thus a complementary transition takes
place and we get the word
, then there will be more
pyrimidines
than purines in the sentential form, thus a complementary transition takes
place and we get the word
![]() .
Here the system has to use the rules
.
Here the system has to use the rules
![]()
![]() and by them
a word is derived which consists of one sub-word
and by them
a word is derived which consists of one sub-word
![]() ,
,
![]() sub-words
sub-words
![]() , and
, and ![]() sub-words
sub-words
![]() , where
, where
![]() . The number
. The number ![]() shows how many times the system used the rule
shows how many times the system used the rule
![]() .
The order of the sub-words is not important, so
we can suppose that the word is in the form of
.
The order of the sub-words is not important, so
we can suppose that the word is in the form of
![]() .
In this word the number of purines (which is
.
In this word the number of purines (which is ![]() )
exceeds the number of pyrimidines
(which is
)
exceeds the number of pyrimidines
(which is ![]() ) by
) by ![]() .
.
In the following, the system uses the rules
![]() and performs exactly
and performs exactly
![]() steps. In each step
steps. In each step ![]() new purines and
new purines and ![]() new pyrimidines are generated,
hence by the end of the
new pyrimidines are generated,
hence by the end of the ![]() th derivation step
there are more pyrimidines than purines in the sentential form.
Therefore here a complementary transition takes place and we get the word
th derivation step
there are more pyrimidines than purines in the sentential form.
Therefore here a complementary transition takes place and we get the word
![]() .
.
Here the system uses the rules
![]() and derives the word
and derives the word
![]() , where
, where
![]() .
.
It is clear that all the words in this form can be generated by
the system (the values of the parameters ![]() and
and ![]() depend on the number
of steps the system makes at the beginning of the derivation and on the
number of positions it uses the rule
depend on the number
of steps the system makes at the beginning of the derivation and on the
number of positions it uses the rule
![]() ). It is also clear
that other words cannot be generated by this system, the derivations have
to follow the above line.
). It is also clear
that other words cannot be generated by this system, the derivations have
to follow the above line.