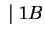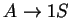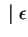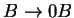|
|
A nagy zh egy jó megoldása
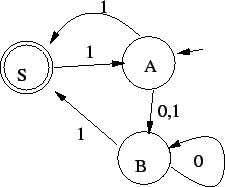
1. Az alábbi automata jó lesz:
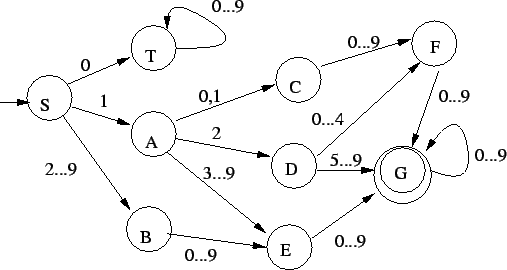
Az állapotok jelentései, ebből adódik, hogy mért jó az automata:
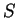 : még nem olvastunk semmit : még nem olvastunk semmit
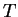 nulla a szám eleje, azaz biztos elutasítunk nulla a szám eleje, azaz biztos elutasítunk
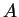 : az első jegy 1 : az első jegy 1
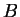 : az első jegy 2-9 : az első jegy 2-9
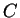 : a szám eleje 10 vagy 11, tehát még legalább két karakter kell az
elfogadáshoz : a szám eleje 10 vagy 11, tehát még legalább két karakter kell az
elfogadáshoz
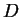 : a szám eleje 12, azaz szét kell majd választani két esetet a következő
karakter szerint : a szám eleje 12, azaz szét kell majd választani két esetet a következő
karakter szerint
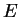 : a szám eleje 13, azaz elég már egy karakter az elfogadáshoz : a szám eleje 13, azaz elég már egy karakter az elfogadáshoz
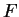 : az első 3 jegy : az első 3 jegy 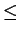 124, azaz még egy karakter kell biztosan 124, azaz még egy karakter kell biztosan
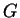 : elfogadó, vagy : elfogadó, vagy 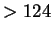 háromjegyű szám jött, vagy egy legalább négyjegyű háromjegyű szám jött, vagy egy legalább négyjegyű
Ez determinisztikus és egy kezdőállapotú, szóval pont, amilyen kell.
2. Az órán tanult algoritmus szerint eljárva:
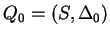 , ahol , ahol
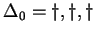
(A falaknál a visszatérő állapotokat 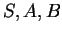 sorrendben sorolom fel, tehát
az első helyen áll az sorrendben sorolom fel, tehát
az első helyen áll az 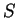 -hez, aztán az -hez, aztán az 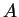 -hoz, végül pedig a -hoz, végül pedig a 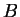 -hez
tartozó visszatérő állapot.) -hez
tartozó visszatérő állapot.)
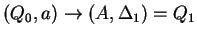 , ahol , ahol
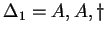
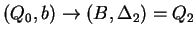 , ahol , ahol
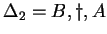
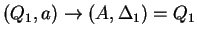
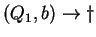
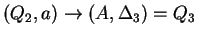 , ahol , ahol
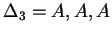
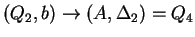
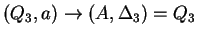
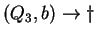
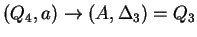
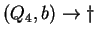
Tehát az egyirányú automata, ami determinisztikus és egy kezdőállapotú:
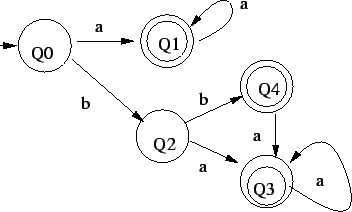
3. Először megfordítjuk a nyelvtant:
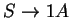 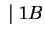
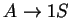 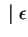
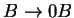 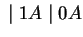
Ezután konstruálunk véges automatát ehhez a megfordított
nyelvtanhoz:
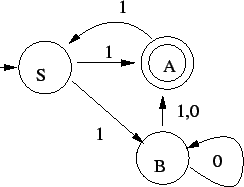
Ezután ezt az automatát visszafordítjuk, azaz a régi kezdőállapot lesz most
az elfogadó, a régi elfogadó állapot a kezdő és minden nyilat fordítva húzunk
be:
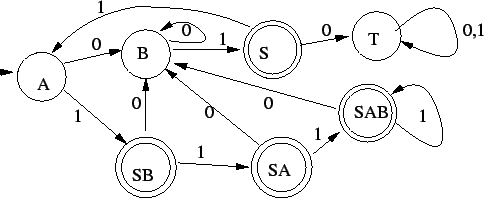
Ezt determinizáljuk és teljesen specifikáljuk:
Ezt még minimalizáljuk, mivel minimálautomata kell:
A=1, B=2, SB=3, S=4, SA=5, SAB=6, T=7 számozással:
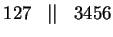
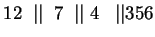
És ez már nem változik, tehát a minimálautomata:
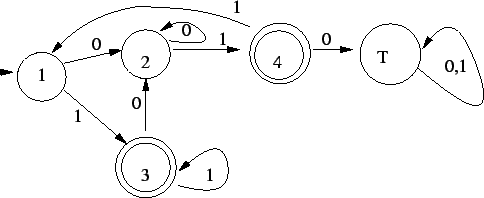
4.
Először minimálautomatát adunk az első reguláris kifejezéshez:
az 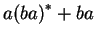 -hoz tartozó automata: -hoz tartozó automata:
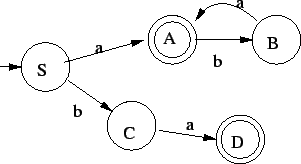
Magyarázat ehhez:
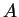 -ban vagyunk, ha -ban vagyunk, ha 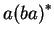 alakú szó jött eddig alakú szó jött eddig
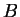 -ben vagyunk, ha -ben vagyunk, ha 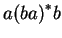 alakú szó jött eddig alakú szó jött eddig
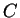 -ben vagyunk, ha egy darab b jött eddig -ben vagyunk, ha egy darab b jött eddig
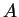 -ban vagyunk, ha egy darab ab jött eddig -ban vagyunk, ha egy darab ab jött eddig
Ebből a tranzitív lezárt automatája, behúzva 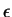 -nyilakat -nyilakat 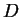 -ből és -ből és
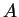 -ból -ból 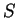 -be és -be és 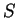 -et elfogadóvá téve
(nem kell új kezdőállapot, mivel a régi kezdőbe nem vezet
vissza nyíl): -et elfogadóvá téve
(nem kell új kezdőállapot, mivel a régi kezdőbe nem vezet
vissza nyíl):
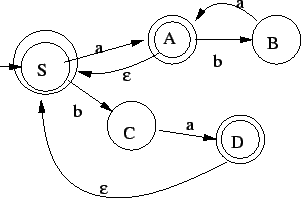
Az 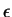 -szabályokat kiküszöbölve: -szabályokat kiküszöbölve:
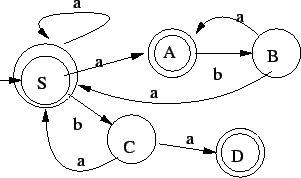
Ezt determinizálva és teljesen specifikálva:
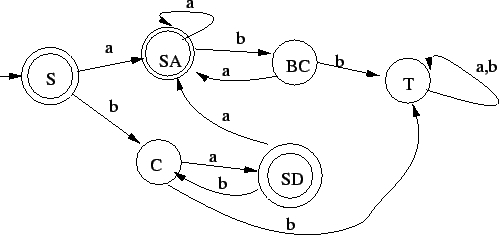
Minimalizálva azt kapjuk, hogy az elfogadók összevonhatók és az
elutasítók is, kivéve a csapdát.
Így lesz a következő automata:
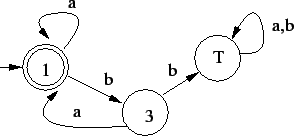
Vagyis az első reguláris kifejezés azokat a szavakat írja le, melyekben minden
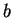 után jönnie kell közvetlenül legalább egy után jönnie kell közvetlenül legalább egy 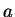 -nak. Másszóval amely szavakban
nincs kettő -nak. Másszóval amely szavakban
nincs kettő 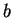 egymás után és ahol a szavak nem is végződhetnek egymás után és ahol a szavak nem is végződhetnek 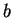 -re. -re.
Megmutatjuk, hogy a második reg. kif. is pont ezeket a szavakat írja le.
Vegyük észre, hogy a második reg. kif. ugyanaz, mint
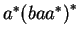 , hiszen , hiszen
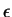 része része 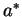 -nak és -nak és
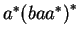 -nak is. -nak is.
Az
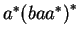 által leírt szavakban nem állhat két által leírt szavakban nem állhat két 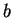 egymás után, mert
minden egymás után, mert
minden 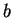 -t követ legalább egy -t követ legalább egy 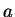 és ugyanezért és ugyanezért 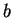 -re se végződhetnek a
szavak. Másrészt minden olyan szót, amiben nincs két -re se végződhetnek a
szavak. Másrészt minden olyan szót, amiben nincs két 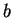 egymás után és ami nem
végződik egymás után és ami nem
végződik 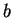 -re leír az -re leír az
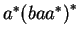 kifejezés, hiszen akárhány kifejezés, hiszen akárhány 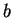 -t és a -t és a
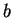 -k után akárhány -k után akárhány 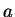 -t le tudunk tenni. -t le tudunk tenni.
Tehát a két reg. kif. azonos nyelvet ad meg.
5. Az 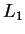 nyelv reguláris, amit az alábbi véges automata bizonyít: nyelv reguláris, amit az alábbi véges automata bizonyít:
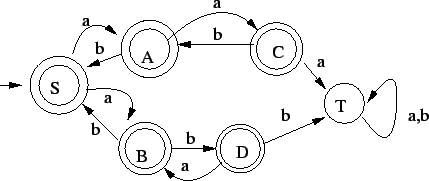
Az állapotok jelentése a következő:
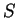 : eddig pont ugyanannyi : eddig pont ugyanannyi 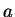 volt, mint volt, mint 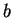
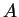 : eddig eggyel több : eddig eggyel több 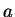 volt, mint volt, mint 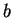
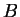 : eddig eggyel több : eddig eggyel több 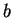 volt, mint volt, mint 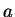
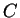 : eddig kettővel több : eddig kettővel több 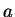 volt, mint volt, mint 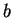
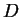 : eddig kettővel több : eddig kettővel több 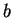 volt, mint volt, mint 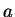
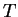 : volt már rossz kezdőszelet, ahol túl nagy volt a különbség, innen már sose
fogadunk el, azaz csapda : volt már rossz kezdőszelet, ahol túl nagy volt a különbség, innen már sose
fogadunk el, azaz csapda
Ez az automata pont a kívánt nyelvet fogadja el, hiszen csak arra
kell figyelni, hogy az eddig beolvasott szóban az 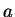 -k és -k és 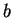 -k számának
különbsége 0, 1, 2, vagy több. -k számának
különbsége 0, 1, 2, vagy több.
Az 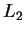 nyelv azonban nem reguláris, ezt a pumpálási lemmával igazoljuk.
Ha nyelv azonban nem reguláris, ezt a pumpálási lemmával igazoljuk.
Ha 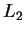 reguláris lenne, akkor létezne egy olyan reguláris lenne, akkor létezne egy olyan 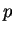 szám, ami a lemmában
van. Vegyük ezen szám, ami a lemmában
van. Vegyük ezen 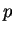 -vel az -vel az 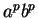 szót. Ez a szó szót. Ez a szó 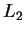 -ben van és
hosszabb -ben van és
hosszabb 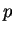 -nél. Jelöljük ki benne az -nél. Jelöljük ki benne az 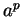 részszót. Mivel ez sem rövidebb részszót. Mivel ez sem rövidebb
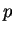 -nél, a lemma miatt ebben kell tudnunk találni egy olyan részszót, melyet
lehet ismételgetni úgy, hogy még mindig a nyelvben maradunk.
De -nél, a lemma miatt ebben kell tudnunk találni egy olyan részszót, melyet
lehet ismételgetni úgy, hogy még mindig a nyelvben maradunk.
De 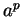 -ben csak csupa -ben csak csupa 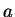 -ból álló részszót tudunk találni, ha pedig azt
több, mint 3-szor megismételjük, akkor biztos több mint kettővel több
lesz az -ból álló részszót tudunk találni, ha pedig azt
több, mint 3-szor megismételjük, akkor biztos több mint kettővel több
lesz az 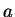 -k száma a szóban, mint a -k száma a szóban, mint a 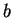 -k száma. -k száma.
|