


Next: About this document ...
A feladat:
(a)
Készíts LR(0) elemzőt az
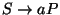 ,
,
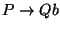 ,
,
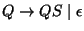 nyelvtanhoz!
nyelvtanhoz!
(b) Elemezd az előbb kapott elemzővel az aabb szót!
(a)
Megoldás:
Először nézzük, hogy a halmazok hogyan jönnek ki:
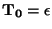 |
T0S=T1 |
T0a=T2 |
| |
|
|
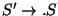 |
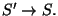 |
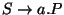 |
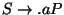 |
|
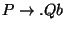 |
| |
|
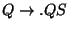 |
| |
|
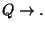 |
| |
|
|
|
T2P=T3 |
T2Q=T4 |
T4b=T5 |
| |
|
|
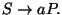 |
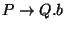 |
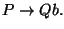 |
| |
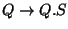 |
|
| |
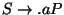 |
|
| |
|
|
|
T4S=T6 |
T4a=T2 |
|
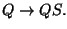 |
|
|
| |
|
|
Magyarázat a halmazokhoz:
T0:
Az
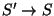 belekerül mindenképpen. Mivel ebben S áll a pont mögött,
a lezáráskor beletesszük a 2. szabályt is.
belekerül mindenképpen. Mivel ebben S áll a pont mögött,
a lezáráskor beletesszük a 2. szabályt is.
T0-ból úgy lépünk tovább, hogy megnézzük, hogy milyen szimbólumok állnak a pont mögött T0-beli
szabályban (most ez a és S) és képezzük a T0 + adott szimbólum
alakú újabb halmazokat, ez most T0S=T1 és T0a=T2. Ezen
halmazok elemeit majd később kiszámoljuk.
T1:
Mivel T1=T0S, az alapító (és egyben egyetlen) elemet úgy kapjuk, hogy
a T0-beli 1. szabályban átemeljük a pontot az S-en.
T2:
Mivel ez a halmaz T0-ból jön a-val, az alapító
eleme az 1. elem lesz.
Ebből lezárással jön a 2. és a 3., végül mind a 2. mind a 3. szabályból jöhet
lezárással a
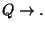 szabály (de persze csak
egyszer írjuk ki), ami a
szabály (de persze csak
egyszer írjuk ki), ami a
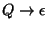 -nak felel meg, de
az
-nak felel meg, de
az 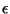 -t nem írjuk, csak a
-t nem írjuk, csak a
 -t.
-t.
T1-ből nem tudunk újabb halmazt származtatni, mert nincs
benne olyan szabály, ahol pont után bármi lenne.
T2-ből jön a T3 (P-vel) és a T4 (Q-val).
T3:
Csak egy elem van, az alpító elem, amit T2-ből kapunk.
T4:
Alapítóként bekerül az első két szabály, aztán a 2. miatt még a 3. is.
T5=T4b és T6=T4S:
Csak egy-egy elemük van, az egy-egy alapító elem,
melyeket T4-ből kapunk.
T4a=T2:
Mert ugyanazok a szabályok jelennek meg, mint T2-ben.
Az elemzőtábla:
| |
|
a |
b |
S |
P |
Q |
| T0 |
S |
T2 |
|
T1 |
|
|
| T1 |
A |
|
|
|
|
|
| T2 |
4 |
|
|
|
T3 |
T4 |
| T3 |
1 |
|
|
|
|
|
| T4 |
S |
T2 |
T5 |
T6 |
|
|
| T5 |
2 |
|
|
|
|
|
| T6 |
3 |
|
|
|
|
|
Magyarázat az elemzőtáblához:
Az ugrórészt aszerint töltjük ki, hogy hogyan származnak egymásból a Ti
halmazok. Például, mivel T0a=T2, ezért a T0-s sorba az a-s oszlopba
azt írjuk, hogy T2.
Az action rész:
Ha van
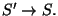 elem egy halmzaban (ilyen a T1, akkor A).
elem egy halmzaban (ilyen a T1, akkor A).
Ha van valami más befejeződő szabály (mint például T2-ben a
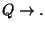 ), akkor a szabály száma (ami itt most a 4).
), akkor a szabály száma (ami itt most a 4).
Ha van pont után terminális valahol, akkor meg S(hift). (Például
T0-ban a 2. szabályban.)
Ha ütközés lenne valahol (két különböző dolgot akarnánk ugyanoda
suvasztani, akkor nem LR(0) elemezhető a nyelvtan, de most itt
ilyen nincsen).
(b)
Az elemzés:
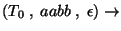
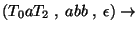
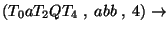
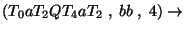
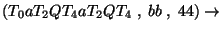
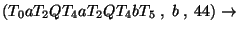
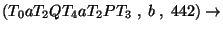
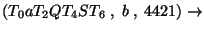
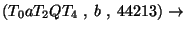
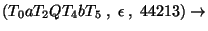
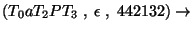
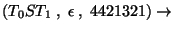 Accept.
Accept.
Pici magyarázat az elemzéshez:
Mindig aszerint cselekszünk, hogy milyen T van a verem tetején
(azaz a verem milyen állapotban van). Ha Ti van a verem tetején, akkor
a Ti-nek megfelelő sor action része játszik.
Ha ez S(hift)
(pl. 1. sor, ahol a T0-ban shiftelni kell), akkor
berakjuk a következő szimbólumot az inputról a verembe, és az
ugrótábla alapján kiszámítjuk az új veremállapotot
(T0-hoz és a-hoz T2 az új állapot).
Ha az action egy letörés (mint például a 6. sorban, a T5
állapotban), akkor
megkeressük a verem tetején a T-k között annak a szabálynak a jobboldalát
ami szerint le akarunk törni (ez most a 2. szabály jobboldala, vagyis
aP), ezt kivesszük a veremből és visszaírjuk a
szabály baloldalát (ez most az S). Ezután kiszámítjuk, hogy
mi lesz az új állapot. Úgy tesszük ezt, hogy megnézzük, hogy milyen
állapotba került a verem, amikor
kivettük a jobboldalt (ez most T4) és megnézzük, hogy
a baloldal hatására (S) mi lesz az új
állapot (az ugrótábla mutatja, hogy
T6).
Ha Accept a tennivaló, akkor befejezzük az elemzést és megállunk.
Még egy nehezebb pont: amikor a 4. szabály szerint törünk le (pl. 2. sor),
akkor a semmit, ami most a szabály jobboldala a verem legtetején
keressük, és helyettesítjük Q-val, a szabály baloldalával.
Ez tehát olyan, mintha csak beraknánk egy Q-t a verem tetejére.



Next: About this document ...
Judit Csima
2000-04-27