


Next: About this document ...
Megoldások a hetedik óra pótgyakorlatához
1. Mivel
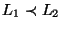 ,
ezért létezik egy olyan f függvény, ami
polinomidőben számolható, azaz van olyan k , hogy x bemenetre f(x)
|x|k időben megvan, és teljesül, hogy
,
ezért létezik egy olyan f függvény, ami
polinomidőben számolható, azaz van olyan k , hogy x bemenetre f(x)
|x|k időben megvan, és teljesül, hogy 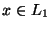 pontosan akkor, ha
pontosan akkor, ha
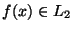 .
Hasonlóan, mivel
.
Hasonlóan, mivel
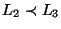 ,
ezért van olyan g, amire
van olyan l szám, hogy y ismeretében g(y) |y|l időben kiszámolható és
,
ezért van olyan g, amire
van olyan l szám, hogy y ismeretében g(y) |y|l időben kiszámolható és
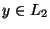 pontosan akkor, ha
pontosan akkor, ha
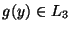 .
Ezután a
.
Ezután a 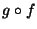 függvény egy Karp redukciója lesz L1-nek L3-ra, mivel
függvény egy Karp redukciója lesz L1-nek L3-ra, mivel
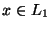 pontosan akkor ha
pontosan akkor ha
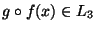 és x ismeretébn
és x ismeretébn
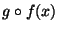 legfeljebb
|x|kl időben kiszámolható.
legfeljebb
|x|kl időben kiszámolható.
2. A nyelv NP-beli, mert a színezés jó lesz tanúnak.
Megmutatjuk, hogy a 3-SZIN problémát vissza lehet vezetni a 4-SZIN
problémára, ez teljessé teszi az állítás igazolását.
A visszavezetés legyen következő: egy G gráfhoz hozzárendeljük azt a G'
gráfot, amit úgy kapunk, hogy G-hez hozzáveszünk egy új pontot és ezt az új pontot
minden G-beli régi ponttal összekötjük.
Ez a leképezés gyorsan számolható: G-ből G'-t megkonstruálni O(n)
lépés.
Ha G-hez van 3 színnel színezés, akkor G'-t ki tudjuk színezni négy színnel:
az új pont kapja a nagyedik színt, mindenki más, meg azt, amit G-ben.
Fordítva, ha G' színezhető 4 színnel, akkor biztos, hogy az új pont színét
egy G-beli pont se kaphatja, ezért a G-beli pontokon csak 3 színt használunk, vagyis
van G-re egy 3 színnel színezésünk.
3. RH1 NP-beli, mert tanúnak jó az az indexhalmaz, amely indexhez
tartozó súlyok kiadják a b-t.
Kell még az, hogy vissza lehet rá vezetni egy NP-teljes problémát:
ez az RH lesz.
A visszavezetés a következő: egy
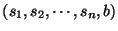 RH kérdéshez
rendeljük hozzá az
RH kérdéshez
rendeljük hozzá az
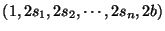 RH1 kérdést.
Ez gyorsan megy (lineáris idő).
Ha az eredeti RH problémának van megoldása, akkor az RH1-nek is van, ugyanazok az indexek jók lesznek.
Ha meg az RH1-esnek van megoldása, akkor az csak úgy lehet, hogy az
1-et nem használtuk, mert minden más súly páros és a 2b is az.
Ekkor viszont a kiválasztott indexek jók az RH probléma megoldására is.
RH1 kérdést.
Ez gyorsan megy (lineáris idő).
Ha az eredeti RH problémának van megoldása, akkor az RH1-nek is van, ugyanazok az indexek jók lesznek.
Ha meg az RH1-esnek van megoldása, akkor az csak úgy lehet, hogy az
1-et nem használtuk, mert minden más súly páros és a 2b is az.
Ekkor viszont a kiválasztott indexek jók az RH probléma megoldására is.
4. A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok
58. feladatnál.
5. Adunk egy lineáris algoritmust. Csinálunk egy szélességi bejárást.
A páratlan szinteket színezzük kékre a párosakat pirosra.
A keresztélek okozhatnak csak bajt: ha van keresztél, akkor nem
lehet jó színezést csinálni, mert akkor van páratlan kör a gráfban.
Ha nem találunk keresztélet, akkor meg végig tudjuk csinálni a
bejárást és így a színezést is.
6. Adunk egy polinomiális algoritmust
(lineáris, ha éllistával adott a gráf, különben négyzetes).
Először nézzük meg, hogy összefüggő-e a gráf. Ha nem, akkor semmilyen fa nincsen, elutasítunk.
Ha összefüggő, akkor hagyjuk el az S halamaz pontjait a
beléjük vezető élekkel együtt és készítsük el a maradék gráf egy feszítőfáját.
Ez eddig lineáris idő.
Ha nincs feszítőfa, csak erdő, azaz a maradék gráf nem összefüggő, akkor
biztosan nincsen olyan fa, amiben az S-beliek elsőfokúak.
Ha van feszítőfa a maradékban, akkor megnézzük, hogy be tudunk-e
kötni minden S-beli pontot egy éllel a fába.
Ha igen, akkor van egy jó fánk, ha nem, akkor az azt jelenti, hogy bizonyos S-beli
pontok csak más S-belieken keresztül kapcsolódnak a maradék gráfhoz, azaz
ekkor az a pont, ahol kapcsolódnak nem lehet első fokú, tehát elutasítjuk a
bemenetet.
Ez az ellenőrzés a végén megvalósítható az S-beli pontok szomszédainak
végignézésével, azi lineáris idő éllista esetén.
7. Visszavezetjük rá a Hamilton-kör problémát. Nagyon
hasonlóan járunk el, mint a 4. feladatnál: egy G gráfhoz
elkészítünk egy G'-t az alábbi módon: felveszünk két új pontot G-n kívül, u-t és v-t.
u-t összekötjük G egy p pontjával, v-t meg a kiválasztott p pont
szomszédaival.
Ezen kívül még kijelöljük S halmaznak a G'-ben az 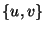 halmazt.
G' konstruálása gyorsan megy.
Ha G-ben volt H-kör, akkor G'-ben lesz olyan fa, aminek elsőfokú csúcsai
u és v: a H-körből elhagyjuk az egyik, a kiválasztott
p ponton át menő, élet
és hozzáveszük a p-u élet és azt a v-be vezető élet,
ami az elhagyott él másik végpontjából indul.
halmazt.
G' konstruálása gyorsan megy.
Ha G-ben volt H-kör, akkor G'-ben lesz olyan fa, aminek elsőfokú csúcsai
u és v: a H-körből elhagyjuk az egyik, a kiválasztott
p ponton át menő, élet
és hozzáveszük a p-u élet és azt a v-be vezető élet,
ami az elhagyott él másik végpontjából indul.
Fordítva: ha van olyan fa G'-ben, amiben csak u és v elsőfokúak, akkor
abban a fában mindenkinek más pont foka 2 kell, hogy legyen.
Van ugyanis összesen n+2 pont, ezen egy fa n+1 élű.
n+1= fokszámok összege osztva kettővel, azaz
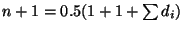 ahol a szummában minden
ahol a szummában minden 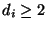 és n tag van. Ebből adódik,
hogy minden di=2. Ez viszont azt jelenti, hogy a fa egy Hamilton út az u és a v pontok között.
A Hamilton út G-beli részéhez hozzávéve egy alkalmas p-re
illeszkedő élet, H-kört kapunk G-ben.
és n tag van. Ebből adódik,
hogy minden di=2. Ez viszont azt jelenti, hogy a fa egy Hamilton út az u és a v pontok között.
A Hamilton út G-beli részéhez hozzávéve egy alkalmas p-re
illeszkedő élet, H-kört kapunk G-ben.
8. A teljes feladatsorban szerepel a megoldás a Bonyolultsági osztályok
47. feladatnál.



Next: About this document ...
Judit Csima
1999-12-16