


Next: About this document ...
Megoldások az első gyakorlathoz
1. Rendezzünk kieséses versenyt az elemek között. Azaz hasonlítsunk
össze két elemet, a kisebbet dobjuk el, a nagyobbat hasonlítsuk egy
új elemhez és ezt ismételgessük, amíg már nincsen új elem. Ami ekkor a
kezünkben van, az a legnagyobb elem.
Ez n-1 összehasonlítás.
Ennél jobbat nem is várhatunk, mert minden összehasonlítás
legfeljebb egy elemet zár ki azok közül, akik még lehetnek legnagyobb
elemek. Az elején n jelölt van, a végén egynek kell maradnia. azaz
n-1 összehasonlítás kell is.
2.
T(n)=3(n-1)+2
(Ezt ellenőrizni is kell: (1) n=1-re jó-e? (2) A rekurziós
formulába visszahelyettesitve jó-e?)
3.
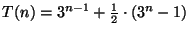
Ellenőrzés is kell!!!
4.
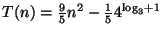
Ellenőrzés!!!
5. (a)
Ha a program lépésszáma n-nel arányos n méretű feladat estén,
akkor az, hogy egy nap alatt megold egy k méretű feladatot,
az azt jelenti, hogy egy nap alatt 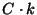 lépést tesz, ahol C>0
egy pozitív konstans. Ha a gép százszor gyorsabb lesz, akkor ezután
lépést tesz, ahol C>0
egy pozitív konstans. Ha a gép százszor gyorsabb lesz, akkor ezután
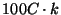 lépést bír tenni. Kérdés, hogy mi az az l méretű
feladat, amire ez elég. Azaz mi az az l, amire
lépést bír tenni. Kérdés, hogy mi az az l méretű
feladat, amire ez elég. Azaz mi az az l, amire
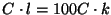 ?
Nyilván l=100k.
?
Nyilván l=100k.
(b)
Hasonlóan gondolkodunk, mint az előbb. Eddig megoldott egy k méretűt
egy nap alatt, tehát bírt lépni Ck3 lépést. A gyors gép
100-szor annyit tud,
100Ck3 lépést egy nap alatt. Ez arra az l méretű feladatra elég,
ahol
Cl3=100Ck3, azaz ahol
![$l=\sqrt[3]{100}k$](img6.gif) .
.
(c)
Hasonlóan: eddig tudott C2k lépést, most tud 100C2k lépést. Ez arra
az l-re elég, ahol
C2l=100C2k, azaz az
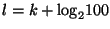 .
.
6. (a)
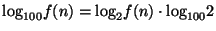 ,
vagyis
,
vagyis
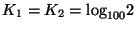 választással
fennáll
választással
fennáll
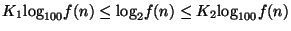 egyenlőtlenség.
egyenlőtlenség.
(b)
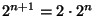 ,
vagyis K1=K2=2 választással
fennáll a
,
vagyis K1=K2=2 választással
fennáll a
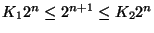 egyenlőtlenség.
egyenlőtlenség.
Másrészt ha
22n=O(2n) lenne, akkor az azt jelentené, hogy van
olyan K>0 szám, hogy
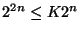 lenne, ekkor viszont
lenne, ekkor viszont
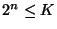 -nek kellene teljesülnie minden n-re, ami nem lehet.
-nek kellene teljesülnie minden n-re, ami nem lehet.
(c)
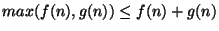 ,
másrészt
,
másrészt
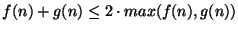 .
Ezekből adódik az állítás, a
.
Ezekből adódik az állítás, a
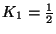 ,
K2= 1 választással.
,
K2= 1 választással.
7. A teljes feladatsorban szerepel a megoldás a Rendezés 15. feladatnál.
8. A teljes feladatsorban szerepel a megoldás a Rendezés 43. feladatnál.
9. Benne van a jegyzetben a megoldás.
10.
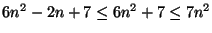 ,
ha
,
ha 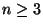 ,
azaz K2=7 jó választás.
Másrészt
,
azaz K2=7 jó választás.
Másrészt
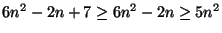 ,
ha
,
ha 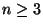 ,
tehát
K1=5 jó lesz.
,
tehát
K1=5 jó lesz.



Next: About this document ...
Judit Csima
1999-11-10