


Next: About this document ...
Algoritmuselmélet pótgyakorlat a harmadik gyakorlathoz
1. A következőket tudjuk egy fa m,n elemeiről: m megelőzi n-t a fa
X-order szerinti bejárásában, viszont m az n után jön a fa Y-order
szerinti bejárásában (X,Y
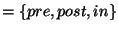 ). Melyik eset(ek)ben tudjuk
eldönteni, hogy m őse-e n-nek?
). Melyik eset(ek)ben tudjuk
eldönteni, hogy m őse-e n-nek?
2. Az S1 és S2 kulcshalmazokat kiegészített 2-3-fákban tároljuk.
Ezek az eredeti 2-3-fától abban különböznek csak, hogy minden csúcsban
fel van jegyezve az onnan induló részfa magassága (szintjeinek száma).
Tegyük még fel, hogy az S1-beli kulcsok mind kisebbek az
S2-belieknél. Javasoljunk hatékony algoritmust a két fa egyesítésére.
A cél tehát egy olyan kiegészített 2-3-fa, amelyben a kulcsok
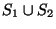 elemei.
elemei.
3. Egy AVL-fába egy új elemet illesztettünk be az előadáson tanult
módszerrel. Az eredményképpen kapott AVL-fa magassága nagyobb, mint
az eredetié. Milyen forgatást alkalmazhattunk?
4. Adott egy n=2k-1 pontú teljes bináris keresőfa. A fában tárolt elemek
egészek az I=[1,2k] intervallumból és egy szám legfeljebb egyszer
fodul elő a fában. Utóbbi feltétel szerint pontosan egy olyan 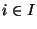 egész van, amely nincs a fában. Adjunk egy hatékony módszert
i meghatározására.
egész van, amely nincs a fában. Adjunk egy hatékony módszert
i meghatározására.
5. Adottak a sík egész koordinátájú
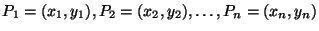 pontjai. Javasoljunk
pontjai. Javasoljunk
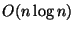 költségű módszert
annak eldöntésére, hogy vannak-e olyan Pi,Pj pontok
(
költségű módszert
annak eldöntésére, hogy vannak-e olyan Pi,Pj pontok
(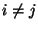 ), melyek távolsága nem több mint 2.
), melyek távolsága nem több mint 2.
6. Egy rendezett halmaz adott n eleméből kupacot szeretnénk építeni, melyre
(a kupac tulajdonság mellett) teljesül, hogy minden x csúcs bal
részfájának az elemei kisebbek mint az x jobb részfájának az elemei.
Igazoljuk, hogy ehhez legalább
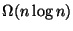 összehasonlítás
szükséges!
összehasonlítás
szükséges!
Algoritmuselmélet pótgyakorlat a harmadik gyakorlathoz
1. A következőket tudjuk egy fa m,n elemeiről: m megelőzi n-t a fa
X-order szerinti bejárásában, viszont m az n után jön a fa Y-order
szerinti bejárásában (X,Y
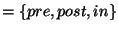 ). Melyik eset(ek)ben tudjuk
eldönteni, hogy m őse-e n-nek?
). Melyik eset(ek)ben tudjuk
eldönteni, hogy m őse-e n-nek?
2. Az S1 és S2 kulcshalmazokat kiegészített 2-3-fákban tároljuk.
Ezek az eredeti 2-3-fától abban különböznek csak, hogy minden csúcsban
fel van jegyezve az onnan induló részfa magassága (szintjeinek száma).
Tegyük még fel, hogy az S1-beli kulcsok mind kisebbek az
S2-belieknél. Javasoljunk hatékony algoritmust a két fa egyesítésére.
A cél tehát egy olyan kiegészített 2-3-fa, amelyben a kulcsok
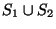 elemei.
elemei.
3. Egy AVL-fába egy új elemet illesztettünk be az előadáson tanult
módszerrel. Az eredményképpen kapott AVL-fa magassága nagyobb, mint
az eredetié. Milyen forgatást alkalmazhattunk?
4. Adott egy n=2k-1 pontú teljes bináris keresőfa. A fában tárolt elemek
egészek az I=[1,2k] intervallumból és egy szám legfeljebb egyszer
fodul elő a fában. Utóbbi feltétel szerint pontosan egy olyan 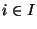 egész van, amely nincs a fában. Adjunk egy hatékony módszert
i meghatározására.
egész van, amely nincs a fában. Adjunk egy hatékony módszert
i meghatározására.
5. Adottak a sík egész koordinátájú
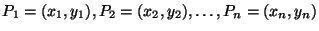 pontjai. Javasoljunk
pontjai. Javasoljunk
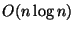 költségű módszert
annak eldöntésére, hogy vannak-e olyan Pi,Pj pontok
(
költségű módszert
annak eldöntésére, hogy vannak-e olyan Pi,Pj pontok
(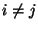 ), melyek távolsága nem több mint 2.
), melyek távolsága nem több mint 2.
6. Egy rendezett halmaz adott n eleméből kupacot szeretnénk építeni, melyre
(a kupac tulajdonság mellett) teljesül, hogy minden x csúcs bal
részfájának az elemei kisebbek mint az x jobb részfájának az elemei.
Igazoljuk, hogy ehhez legalább
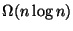 összehasonlítás
szükséges!
összehasonlítás
szükséges!



Next: About this document ...
Judit Csima
1999-10-21