


Next: About this document ...
Algoritmuselmélet gyakorlat (1)
1999. szeptember 13., hétfő
1. Hány összehasonlítással lehet megtalálni n különböző elem közül
a legnagyobbat?
(Úgy értve, hogy mennyi elég biztosan és mennyi kell biztosan.
Tehát ez két kerdés.)
2. Adjuk meg azt a T(n) függvényt zárt alakban, amely a nemnegatív
egész számokon van értelmezve és eleget tesz a következő feltételeknek:
T(1)=2 és 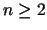 esetén
T(n)=T(n-1)+3
esetén
T(n)=T(n-1)+3
3. Ugyanaz a feladat, mint az előbb, csak most
T(1)=2 és 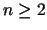 esetén
T(n)=3T(n-1)+1
esetén
T(n)=3T(n-1)+1
4. Ezt kell otthon megoldani és beadni írásban
Adjuk meg azt a T(n) fűggvényt zárt alakban, amely a 3k alakú
számokon van értelmezve és eleget tesz a következő feltételeknek:
T(1)=1 és 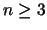 esetén
T(n)=4T(n/3)+n2.
esetén
T(n)=4T(n/3)+n2.
(Segítség: gondoljunk arra, hogy n=3k valami k-ra + a mértani sor
összegképlete.)
5. Tegyük fel, hogy van egy számítógépes programunk, ami egy k
méretű
feladaton a jelenlegi gépünkön 1 nap alatt fut le. Beszereztünk egy
százszor gyorsabb számítógépet. Ugyanazon programmal mekkora
feladatot lehet az új gépen egy nap alatt megoldani, ha a program
lépésszáma n méretű feladat esetén
(a) n-nel
(b) n3-bel
(c) 2n-nel
arányos?
6. Bizonyítsuk be, hogy
7. Négy elem rendezéséhez hány összehasonlítás kell?
Gondolkozni való feladat
8. (a) (*)
Javasoljunk egy olyan algoritmust, ami
 összehasonlítással megtalálja egy n-elemű halmaz legnagyobb és
legkisebb elemét!
összehasonlítással megtalálja egy n-elemű halmaz legnagyobb és
legkisebb elemét!
(b) (**)
Igazoljuk, hogy
 összehasonlítás szükséges is a fenti feladat
megoldására!
összehasonlítás szükséges is a fenti feladat
megoldására!
Gyakorlásnak
9. Tegyük fel, hogy a T(n) függvény csak a 2k alakú számokon van értelmezve
és tudjuk róla, hogy
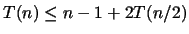 .
Mutassuk meg, hogy
.
Mutassuk meg, hogy
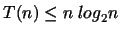 fennáll!
fennáll!
10. Bizonyítsuk be, hogy
(a)

(b)
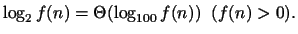



Next: About this document ...
Csiga
1999-09-19