


Next: About this document ...
Algoritmuselmélet gyakorlat (7)
1. Jelölje |x|, ill. C(x) az
 szó hosszát, ill.
Kolmogorov-bonyolultságát. Bizonyítsuk be, hogy:
szó hosszát, ill.
Kolmogorov-bonyolultságát. Bizonyítsuk be, hogy:
(a)
 és x-ben pontosan 20 db 1-es van
és x-ben pontosan 20 db 1-es van

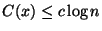 alkalmas c konstansra.
alkalmas c konstansra.
(b)
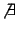 TG, mely n inputtal olyan n hosszú
TG, mely n inputtal olyan n hosszú
 szót
számol ki, melyre
szót
számol ki, melyre
 .
.
(c)
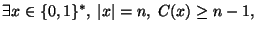 és x 0-val
kezdődik.
és x 0-val
kezdődik.
(d)
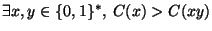 .
"A Kolmogorov-bonyolultság nem monoton a prefixeken."
.
"A Kolmogorov-bonyolultság nem monoton a prefixeken."
2. Az 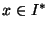 szó xf fordítottja az x betűinek fordított
sorrendben való leírásával kapott szó. Például
11010f=01011.
Mutassuk meg, hogy van olyan c állandó, hogy
|C(x)-C(xf)|<c
teljesül minden
szó xf fordítottja az x betűinek fordított
sorrendben való leírásával kapott szó. Például
11010f=01011.
Mutassuk meg, hogy van olyan c állandó, hogy
|C(x)-C(xf)|<c
teljesül minden 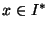 szóra!
szóra!
3. Igazoljuk, hogy tetszőleges n természetes számhoz megadható olyan
 szó, melyre teljesül, hogy
szó, melyre teljesül, hogy
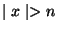 és
és
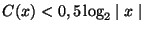 .
.
4. Legyen 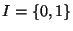 .
A
.
A
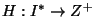 függvény az
függvény az 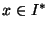 szóhoz azon
szóhoz azon  összenyomhatatlan szavak számát rendeli, amelyek
a kanonikus sorrendben megelőzik x-et. Igaz-e, hogy H rekurzív
függvény?
összenyomhatatlan szavak számát rendeli, amelyek
a kanonikus sorrendben megelőzik x-et. Igaz-e, hogy H rekurzív
függvény?
5. Igazoljuk, hogy ha
 egy véges nyelv, akkor L
felismerhető egy O(n) időkorlátos TG-vel.
egy véges nyelv, akkor L
felismerhető egy O(n) időkorlátos TG-vel.
6. Tegyük fel, hogy van egy olyan K nevű eljárás, mely
(egyetlen lépésben) megmondja, hogy az inputjaként magadott
irányítatlan gráf színezhető-e három színnel.
Csináljunk egy a K eljárást használó algoritmust,
mely polinomidőben megadja az input G gráf egy 3-színezését,
ha
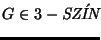 .
.
7. Egy
 nyelv esetén az L* nyelv definíciója a következő:
nyelv esetén az L* nyelv definíciója a következő:
 és van olyan
és van olyan 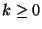 egész és
egész és
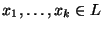 hogy
hogy
 .
.
Igazoljuk, hogy ha  ,
akkor
,
akkor 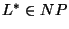 .
.
8. Igazoljuk, hogy az alábbi L nyelv NP-ben van:
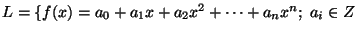 és az f(x)=0
egyenletnek van egész megoldása
és az f(x)=0
egyenletnek van egész megoldása 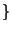 .
.
Megjegyzés: az ai számokat az inputban binárisan ábrázoljuk.
9. Álljon az L nyelv azon G=G(V,E) irányítatlan gráfokból,
melyeknek a V csúcshalmaza felosztható két olyan nemüres
V1 ill.
V2 részre (
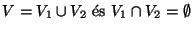 ), hogy
G-nek legfeljebb két V1 és V2 között menő éle
(olyan, aminek az egyik végpontja V1-be, a másik V2-be esik)
van! Bizonyítsuk be, hogy
), hogy
G-nek legfeljebb két V1 és V2 között menő éle
(olyan, aminek az egyik végpontja V1-be, a másik V2-be esik)
van! Bizonyítsuk be, hogy
 !
!



Next: About this document ...
Judit Csima
1999-12-09