


Next: About this document ...
Algoritmuselmélet gyakorlat (5)
1. A 6 pontú G gráf csúcsait jelölje
x,y,z,u,v,w.
A gráf egy mélységi bejárásánál a mélységi, ill. a befejezési számok a
következők:
x: 1,6; y: 2,4; z: 6,5; u: 3,3; v: 4,1; w: 5,2.
Adjuk meg a bejáráshoz tartozó mélységi feszítőfa éleit.
Rekonstruálható-e G az előző számok ismeretében?
2. G irányítatlan gráf a következő éllistával (zárójelben a költségek,
az élek mindkét végpontjukból fel vannak sorolva):
a:b(2),c(3);
b:a(2),d(2);
c:a(3),d(1);
d:b(2),c(1),e(2),f(4);
e:d(2),f(1),g(2);
f:d(4),e(1),g(2),h(1);
g:e(2),f(2),h(3);
h:f(1),g(3);
Keressünk G-ben
(a)
Prim algoritmusával minimális költségű feszítőfát!
(b) Kruskal algoritmusával minimális költségű feszítőfát!
(c) a-ból kiinduló mélységi feszítőfát!
(d) a-ból kiinduló szélességi feszítőfát!
(e) Határozzuk meg G artikulációs pontjait!
3. Adjuk meg az összes olyan minimális élszámú irányított
gráfot (élsúlyokkal együtt), amely(ek)re az alábbi táblázat a
Dijkstra-algoritmusban szereplő D[ ] tömb változásait mutathatja.
Adja meg a legrövidebb utakat tartalmazó P[ ] tömb állapotait is.
| v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
| 0 |
2 |
6 |
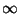 |
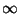 |
7 |
| 0 |
2 |
5 |
9 |
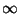 |
6 |
| 0 |
2 |
5 |
6 |
9 |
6 |
| 0 |
2 |
5 |
6 |
8 |
6 |
| 0 |
2 |
5 |
6 |
7 |
6 |
4. Tegyük fel, hogy G egy összefüggő irányítatlan gráf, melynek minden
mélységi feszítőfája egy egyszerű irányított út.
(a)
Igazoljuk, hogy nincs G-nek artikulációs pontja
(olyan csúcsa, melyet az összes belőle induló éllel együtt
elhagyva G-ből, a kapott gráf már nem lesz összefüggő)!
(b)
Mutassuk meg, hogy G nem szükségképpen teljes gráf!
5. Adott éllistával egy n pontú, e élű G
összefüggő irányítatlan gráf. Adjunk
O(e) uniform költségű algoritmust olyan
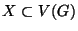 központi
ponthalmaz keresésére, melyre
központi
ponthalmaz keresésére, melyre
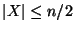 teljesül! Az
teljesül! Az
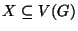 egy központi ponthalmaz, ha G minden pontja vagy
X-beli, vagy egyetlen éllel elérhető valamelyik
X-beli pontból.
egy központi ponthalmaz, ha G minden pontja vagy
X-beli, vagy egyetlen éllel elérhető valamelyik
X-beli pontból.
6. Legyen adott egy 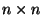 pixelből álló fekete-fehér kép.
Szeretnénk a képen a bal felső saroktól a jobb alsó sarokig
egy jobbra-lefele haladó határvonalat húzni úgy, hogy
a vonaltól jobbra-felfele eső fekete, valamint a vonaltól
balra-lefele eső fehér pixelek számának az összege a lehető
legkisebb legyen. Oldjuk meg ezt a feladatot O(n2)
időben!
pixelből álló fekete-fehér kép.
Szeretnénk a képen a bal felső saroktól a jobb alsó sarokig
egy jobbra-lefele haladó határvonalat húzni úgy, hogy
a vonaltól jobbra-felfele eső fekete, valamint a vonaltól
balra-lefele eső fehér pixelek számának az összege a lehető
legkisebb legyen. Oldjuk meg ezt a feladatot O(n2)
időben!
7. Éllistával adott a súlyozott élű G=(V,E)
gráf. Tegyük fel, hogy az élek súlyai az 1,2,3 számok közül valók.
Javasoljunk O(n+e) uniform költségű algoritmust az 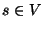 pontból az
összes további
pontból az
összes további 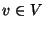 pontokba vivő legrövidebb utak hosszának a
meghatározására. (Itt n a G gráf csúcsainak, e pedig az éleinek a
száma.)
pontokba vivő legrövidebb utak hosszának a
meghatározására. (Itt n a G gráf csúcsainak, e pedig az éleinek a
száma.)
8. A szoftverpiacon n féle grafikus formátum közötti oda-vissza
konverzióra
használatos programok
kaphatók: az i-edik és a j-edik között oda-vissza
fordító program
ára aij, futási ideje pedig tij (ha létezik).
(a) Javasoljunk módszert annak megtervezésére, hogy minden egyes
formátumról a saját grafikus terminálunk által megértett formátumra
a lehető leggyorsabban konvertáljunk! (Az ár nem számít.)
(b) Javasoljunk módszert annak eldöntésére, hogy mely programokat
vásároljuk meg, ha azt szeretnénk a lehető legolcsóbban
megoldani, hogy a megvett programok segítségével
bármelyik formátumról bármelyik más formátumra képesek
legyünk konvertálni. (Itt a futási idő nem számít).
9. Az ország n különböző
 városában ma délután 4-kor
futballmérkőzéseket
fognak játszani. Egy televiziós társaságnak m operatőre van, akikről
tudjuk, hogy délután 2-kor az
városában ma délután 4-kor
futballmérkőzéseket
fognak játszani. Egy televiziós társaságnak m operatőre van, akikről
tudjuk, hogy délután 2-kor az
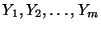 városokban
lesznek. Adott a városok távolsága is, pontosabban ismert,
hogy mennyi
idő alatt lehet Yi-ből Xj-be eljutni. Adjunk hatékony
algoritmust arra, hogy a televiziós társaság minél több mérkőzést
rögzíteni tudjon (az elejétől a végéig)! Elemezzük a
módszer futási idejét!
városokban
lesznek. Adott a városok távolsága is, pontosabban ismert,
hogy mennyi
idő alatt lehet Yi-ből Xj-be eljutni. Adjunk hatékony
algoritmust arra, hogy a televiziós társaság minél több mérkőzést
rögzíteni tudjon (az elejétől a végéig)! Elemezzük a
módszer futási idejét!



Next: About this document ...
Judit Csima
1999-11-10