


Next: About this document ...
Algoritmuselmélet gyakorlat (4)
Alapvetők
1. A hash-függvény legyen f(K)=K, a táblaméret M=7, és
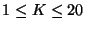 .
Helyezzük el a táblában a 3, 4, 7, 11, 14, 17, 20 kulcsokat ebben
a sorrendben
.
Helyezzük el a táblában a 3, 4, 7, 11, 14, 17, 20 kulcsokat ebben
a sorrendben
(a)
lineáris
(b)
kvadratikus maradék
próbálást használva az ütközések feloldására.
2. Határozzuk meg a BARBARÁNAK szó egy lehetséges
Huffman-kódját és Lempel-Ziv-Welch-kódját. Az utóbbinál tegye
fel, hogy a szótár a kezdőhelyzetben az A, Á, B, K, N, R betűket
tartalmazza, és ezek kódjai rendre 1, 2, 3, 4, 5, 6.
Átlagos feladatok
3. Mi a baja az
 hash-függvénynek, ahol 7 a
táblaméret?
hash-függvénynek, ahol 7 a
táblaméret?
4. Legyen T egy olyan bináris fa, melyben minden nem-levél csúcsnak
pontosan
2 fia van. Igaz-e, hogy van olyan eloszlás, amelyhez tartozó Huffman-fa
éppen T?
5. Az
 háromelemű ábécé mellett futtatjuk a
Lempel-Ziv-Welch algoritmust egy adott szövegre. A tömörítés
egy pontján bekerül a szótárba az xy szó kódja. Amennyiben
később szerepel a szövegben xy részszó, biztos-e,
hogy együtt fogjuk őket kódolni?
háromelemű ábécé mellett futtatjuk a
Lempel-Ziv-Welch algoritmust egy adott szövegre. A tömörítés
egy pontján bekerül a szótárba az xy szó kódja. Amennyiben
később szerepel a szövegben xy részszó, biztos-e,
hogy együtt fogjuk őket kódolni?
6. A T[0:M] táblában 2n elemet helyeztünk el az első 3n
helyen (3n<M) egy ismeretlen hash-függvény segítségével.
A táblában minden 3i indexű hely üresen maradt (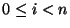 ).
Legfeljebb hány ütközés lehetett, ha az ütközések
feloldására
).
Legfeljebb hány ütközés lehetett, ha az ütközések
feloldására
a) lineáris próbálást
b) kvadratikus maradék próbálást használtunk?
7. A
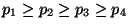 valószínűség-eloszláshoz ketten
készítettek Huffman-kódot.
Egyikük kódszavai: 0, 10, 110, 111; másikukéi: 00, 01, 10, 11.
Tudva, hogy p3=1/6, határozzuk meg p1,
p2, p3 és p4 értékét.
valószínűség-eloszláshoz ketten
készítettek Huffman-kódot.
Egyikük kódszavai: 0, 10, 110, 111; másikukéi: 00, 01, 10, 11.
Tudva, hogy p3=1/6, határozzuk meg p1,
p2, p3 és p4 értékét.
8. A
 ábécé feletti szövegeket Huffman és
Lempel-Ziv-Welch módszerrel is kódoljuk. A Lempel-Ziv szótárban
minden karaktersorozatnak 8 bites kódot adunk. Lesz-e így a szövegek
között olyan, amelynek a Lempel-Ziv kódja rövidebb lesz a
Huffman-kódjánál?
ábécé feletti szövegeket Huffman és
Lempel-Ziv-Welch módszerrel is kódoljuk. A Lempel-Ziv szótárban
minden karaktersorozatnak 8 bites kódot adunk. Lesz-e így a szövegek
között olyan, amelynek a Lempel-Ziv kódja rövidebb lesz a
Huffman-kódjánál?
9. A T[0:M-1] táblában rekordokat tárolunk nyitott címzésű
hashelt
szervezéssel. Az ütközések feloldására lineáris próbálást
alkalmazunk.
Tehát ha a h(K) sorszámú cella foglalt, akkor a K kulcsú rekordot
a
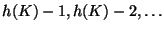 sorszámú cellák közül az első üresbe
tesszük.
Tegyük fel, hogy a tábla használata során egy hibás törlés történt:
egy cellából kitöröltünk egy rekordot a törlés-bit beállítása nélkül.
sorszámú cellák közül az első üresbe
tesszük.
Tegyük fel, hogy a tábla használata során egy hibás törlés történt:
egy cellából kitöröltünk egy rekordot a törlés-bit beállítása nélkül.
(a)
Igaz-e, hogy a hibás törlés helye mindig megtalálható?
(b)
Adjunk hatékony (lineáris időigényű) algoritmust a tábla
megjavítására. (Módosítsuk úgy a
táblát, hogy megszűnjenek a hibás
törlés negatív következményei.)
10. Egy S szöveg tömörítésére a Lempel-Ziv-Welch módszert alkalmaztuk.
Azt tapasztaltuk, hogy a kódolás során használt szótárban
előfordult 100 betűből álló szó. Adjunk minél jobb alsó becslést
az S szöveg hosszára!
Nehézke
11. A
 eloszlásokhoz Huffman-kódot
készítettünk. Mekkora lehet p1 lehető legnagyobb értéke,
ha a kapott kódszavak a következők:
eloszlásokhoz Huffman-kódot
készítettünk. Mekkora lehet p1 lehető legnagyobb értéke,
ha a kapott kódszavak a következők:



Next: About this document ...
Judit Csima
1999-10-29