


Next: About this document ...
Algoritmuselmélet gyakorlat (3)
Elemi alapfeladatok
1. Bizonyísuk be, hogy az inorder bejárás növekvő sorrendben adja vissza egy
bináris fa elemeit!
2. Egy bináris keresőfa "valamely bejárásán" mindig a
 -order valamelyikét értjük.
-order valamelyikét értjük.
(a) Mely bejárásoknál lehetséges az, hogy a tárolt
elemek legnagyobbika megelőzi a legkisebbet?
(b) Tegyük fel, hogy egy bináris keresőfában az
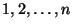 számok vannak tárolva, továbbá hogy a fa valamely bejárásánal
a számok az
számok vannak tárolva, továbbá hogy a fa valamely bejárásánal
a számok az
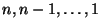 sorrendben következnek. Határozzuk meg,
melyik lehetett ez a bejárás és milyen lehetett ez a bináris keresőfa!
sorrendben következnek. Határozzuk meg,
melyik lehetett ez a bejárás és milyen lehetett ez a bináris keresőfa!
3. Illesszük be az alábbi 6 kulcsot egy kezdetben üres (2,3)-fába
a megadott sorrendben:
D,B,E,A,C,F. Rajzoljuk le az eredményül kapott fát!
4. Építsünk AVL-fát az alábbi input számsorozatból:
4,3,2,1,7,6,5.
Normális feladatok
5. Egy bináris keresőfa csúcsait egy, a gyökértől egy levélig menő út
szerint három osztályba soroljuk:
B az úttól balra levő,
U az útra eső, J pedig az úttól jobbra
levő csúcsok halmazát jelöli.
Igaz-e mindig, hogy minden B-beli csúcs kulcsa
kisebb tetszőleges U-beli csúcs kulcsánál,
és minden U-beli csúcs kulcsa
kisebb, mint tetszőleges J-beli csúcs kulcsa?
6. Egy rendezett univerzum n eleme egy A bináris keresőfában,
k eleme pedig egy B bináris keresőfában van tárolva. Adjunk
minél hatékonyabb módszert a két fában levő elemek nagyság szerinti
sorrendben történő kilistázására! (Tehát egy olyan tömböt szeretnénk
kapni, amiben az n+k elem rendezetten helyezkedik el.)
Elemezzük a módszer költségét!
7. Az [1,178] intervallum összes egészei egy
2-3 fában helyezkednek el. Tudjuk, hogy a
gyökérben két kulcs van, és az első kulcs a 17. Mi lehet a második?
Miért?
8. Adott n pont a síkon, melyek páronként mindkét
koordinátájukban
különböznek. Bizonyítsuk be, hogy egy és csak egy bináris
fa létezik, melynek szögpontjai az adott n pont, és az első
koordináta szerint a keresőfa tulajdonsággal, a második
szerint pedig a kupac tulajdonsággal rendelkezik.
(Vigyázat: a kupac
tulajdonságba nem értendő bele, hogy a fa teljes bináris fa
legyen, mint amilyet a tanult "kupacépítő" algoritmus létrehoz.)
9. Adjunk példát olyan AVL fára, hogy egy alkalmas törlés esetén
egyetlen forgatás ne legyen elegendő az AVL-tulajdonság
helyreállítására.
10. Adott egy n pontú AVL-tulajdonágú bináris fa.
Adjunk meg polinomidejű algoritmust az
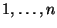 számok egy olyan sorrendjének meghatározására,
amely esetén az AVL-fa építő algoritmus a megadott
fát hozza létre, mégpedig forgatás nélkül.
számok egy olyan sorrendjének meghatározására,
amely esetén az AVL-fa építő algoritmus a megadott
fát hozza létre, mégpedig forgatás nélkül.
Gondolkozni való feladat
11. Adott n chip, melyek képesek egymás tesztelésére a következő
módon:
ha összekapcsolunk két chipet, mindkét chip nyilatkozik a másikról, hogy
hibásnak találta-e. Egy hibátlan chip korrektül felismeri, hogy a másik
hibás -e, míg egy hibás chip akármilyen választ adhat. Tegyük fel, hogy
a chipek több, mint a fele korrekt. Adjunk algoritmust, mely n-nél kevesebb
fenti tesztet használva kikeres egy jó chipet.



Next: About this document ...
Judit Csima
1999-10-14