


Next: About this document ...
Algoritmuselmélet gyakorlat (2)
1. Legyen adott egy egészekből álló A[1:n]
tömb valamint egy b egész szám. Szeretnénk
hatékonyan eldönteni, hogy
van-e két olyan
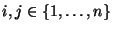 index,
melyekre
A[i]+A[j]=b. Oldjuk meg ezt a feladatot
index,
melyekre
A[i]+A[j]=b. Oldjuk meg ezt a feladatot
 időben!
időben!
2. A (növekvően) rendezett A[1:n] tömb
k darab elemét valaki megváltoztatta. A változtatások helyeit
nem ismerjük. Javasoljunk
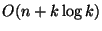 uniform költségű algoritmust az így módosított tömb rendezésére!
uniform költségű algoritmust az így módosított tömb rendezésére!
3. Adott egy rendezett univerzum n különböző eleméből álló
S halmaz. Legyen
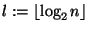 .
Felosztandó
az S halmaz olyan nem üres
.
Felosztandó
az S halmaz olyan nem üres
 részhalmazokra, hogy
tetszőleges
részhalmazokra, hogy
tetszőleges
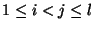 számpárra az Si halmaz
minden eleme kisebb legyen az Sj halmaz minden eleménél.
Adjunk meg egy
számpárra az Si halmaz
minden eleme kisebb legyen az Sj halmaz minden eleménél.
Adjunk meg egy
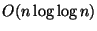 összehasonlítást használó
módszert a fenti feladatra!
összehasonlítást használó
módszert a fenti feladatra!
4. Adott egy egész számokat tartalmazó A[1:n] tömb, amelyben legfeljebb
n elempár áll inverzióban egymással. (Két elem akkor áll inverzióban, ha a nagyobb
megelőzi a kisebbet.) Igaz-e, hogy a buborékrendezés rendezi a tömböt
(a) legfeljebb n összehasonlítással?
(b) legfeljebb n cserével?
5. Adjunk konstans szorzó erejéig optimális számú
összehasonlítást használó módszert az
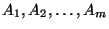 egyenként k elemű rendezett tömbök összefésülésére!
egyenként k elemű rendezett tömbök összefésülésére!
6. Adjunk hatékony algoritmust egy kupac tizedik legkisebb elemének a
megtalálására. Elemezzük a módszer költségét.
7. Egy rendezett halmazból n elem kupacban van elhelyezve. Bizonyítsuk be,
hogy a legnagyobb elem megkereséséhez 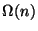 összehasonlítás
szükséges!
összehasonlítás
szükséges!
8. Adott egy dobozban n különböző méretű anyacsavar,
valamint egy másik dobozban a
hozzájuk illő apacsavarok.
Kizárólag a következő összehasonlítási lehetőségünk van:
Egy apacsavarhoz hozzápróbálunk egy anyacsavart. A próbának háromféle kimenete
lehet:
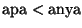 ,
,
 ,
vagy
,
vagy
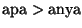 ;
annak megfelelően, hogy
az apacsavar külső átmérője hogyan viszonyul az anyacsavar belső
átmérőjéhez.
Szeretnénk az anyacsavarokhoz megtalálni a megfelelő apacsavarokat.
Adjunk erre a feladatra átlagosan
;
annak megfelelően, hogy
az apacsavar külső átmérője hogyan viszonyul az anyacsavar belső
átmérőjéhez.
Szeretnénk az anyacsavarokhoz megtalálni a megfelelő apacsavarokat.
Adjunk erre a feladatra átlagosan
 összehasonlítást
felhasználó módszert!
összehasonlítást
felhasználó módszert!
9. Vázoljunk egy O(n) időigényű algoritmust
(az időkorlát bizonyításával
együtt) n olyan egész számból álló sorozat rendezésére,
melynek elemei az
(a)
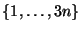 tartományba esnek!
tartományba esnek!
(b)(*)
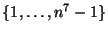 tartományba esnek!
tartományba esnek!
10. Adottak a sík egész koordinátájú
 pontjai. Javasoljunk O(n) uniform költségű módszert olyan
pontjai. Javasoljunk O(n) uniform költségű módszert olyan
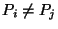 pontok kiválasztására, amelyeken átmenő egyenes által
meghatározott félsíkok közül az egyik tartalmazza az összes input
pontot.
pontok kiválasztására, amelyeken átmenő egyenes által
meghatározott félsíkok közül az egyik tartalmazza az összes input
pontot.
11. Valaki egy összehasonlításon alapuló állítólagos rendezési algoritmusról azt
mondja,
hogy mivel az eljárás minden olyan sorozatot jól rendez, amelyben a rendezett
sorrendhez képest csak egyetlen pár van felcserélve, ezért az algoritmus tetszőleges
soroztot rendez. Helyes-e ez a következtés?
Gondolkozni való feladat
12. Hány összehasonlítással lehet rendezni öt elemet?
13. Egy n-szer n-es táblázatban úgy van elhelyezve
n2 db különböző szám, hogy mind a sorok mind az oszlopok
monoton növekvőek. Mutassuk meg, hogy ekkor a keresés
lépésszáma 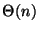 .
.



Next: About this document ...
Judit Csima
1999-09-30